Corrigé de l'exercice 3 du bac ES de maths de mai 2012 au Liban
Cacher les corrigés
Dans un salon de coiffure pour femmes, le coloriste propose aux clientes qui viennent pour une coupe deux prestations supplémentaires :- une coloration naturelle à base de plantes qu'il appelle « couleur-soin »,
- des mèches blondes pour donner du relief à la chevelure, qu'il appelle « effet coup de soleil ».
- 40 % des clientes demandent une « couleur-soin »,
- parmi celles qui n'en veulent pas, 30 % demandent un « effet coup de soleil »,
- de plus, 24 % des clientes demandent les deux à la fois.
1. Calculer la probabilité de M sachant C notée
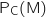 .
.
La formule des probabilités conditionnelles donne :
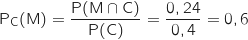 .
.
2. Construire un arbre pondéré qui illustre la situation.
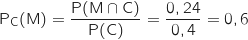 .
.
3. Calculer la probabilité que la cliente ne souhaite ni une « couleur-soin », ni un « effet coup de soleil ».
En utilisant la formule des probabilités composées on a :
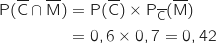
4. Montrer que la probabilité de l'évènement M est égale à 0,42.
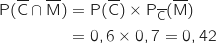
Les événements C et 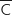 constituent un système complet d'événements et d'après la formule des probabilités totales on a :
constituent un système complet d'événements et d'après la formule des probabilités totales on a :
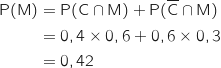
5. Les évènements C et M sont-ils indépendants ?
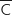 constituent un système complet d'événements et d'après la formule des probabilités totales on a :
constituent un système complet d'événements et d'après la formule des probabilités totales on a :
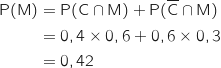
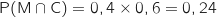
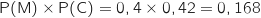 Donc
Donc 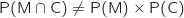 ce qui montre que M et C ne sont pas indépendants.
ce qui montre que M et C ne sont pas indépendants.
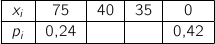

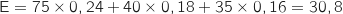
L'espérance à atteindre est : 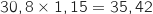 .
On cherche le prix
.
On cherche le prix  du « coup de soleil » tel que :
du « coup de soleil » tel que :
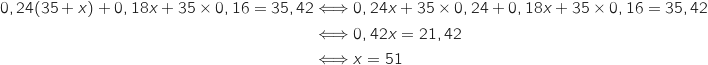 Donc le coloriste doit facturer le « coup de soleil » 51 euros.
Donc le coloriste doit facturer le « coup de soleil » 51 euros.
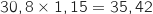 .
On cherche le prix
.
On cherche le prix  du « coup de soleil » tel que :
du « coup de soleil » tel que :
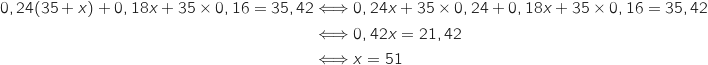 Donc le coloriste doit facturer le « coup de soleil » 51 euros.
Donc le coloriste doit facturer le « coup de soleil » 51 euros.
