Sujet et corrigé de l'exercice 1 du bac ES de maths de mai 2013 au Liban
Cacher les corrigés
Cet exercice est un QCM (questionnaire à choix multiples). Pour chacune des questions posées, une seule des quatre réponses est exacte. Recopier le numéro de la question et la réponse exacte. Aucune justification n'est demandée. Une réponse exacte rapporte 1 point, une réponse fausse ou l'absence de réponse ne rapporte ni n'enlève aucun point.
1. Parmi toutes les fonctions définies sur
et dont l'expression algébrique est donnée ci-dessous, la seule qui est convexe est:
Puisqu'on ne demande aucune justification on peut se contenter d'utiliser la calculette pour « voir » laquelle des courbes représentatives correspond
à une fonction convexe sur .
La bonne réponse est la réponse d.
Si on veut justifier, on peut déjà éliminer la réponse b. car on sait que la fonction logarithme est concave. De même on élimine c.
car la fonction exponentielle est convexe, mais son opposée est concave. Il reste donc à trancher entre a. et d.
Pour a., la dérivée est la fonction 
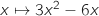et la dérivée seconde est la fonction 
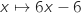, cette dernière ne garde pas un signe constant
sur , donc la fonction proposée en a. n'est ni convexe ni concave sur . Du coup par élimination il ne reste que la réponse d.
2. Une primitive de .
La bonne réponse est la réponse d.
Si on veut justifier, on peut déjà éliminer la réponse b. car on sait que la fonction logarithme est concave. De même on élimine c.
car la fonction exponentielle est convexe, mais son opposée est concave. Il reste donc à trancher entre a. et d.
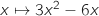Pour a., la dérivée est la fonction et la dérivée seconde est la fonction 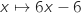, cette dernière ne garde pas un signe constant
sur , donc la fonction proposée en a. n'est ni convexe ni concave sur . Du coup par élimination il ne reste que la réponse d.
sur définie par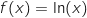 
est la fonction 
définie par :
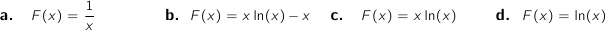
Il suffit de dériver chacune des fonctions proposées.
Pour a. : 
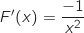donc c'est pas bon.
Pour b. :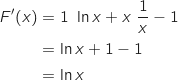 
Donc la bonne réponse est la réponse b.
proposées.
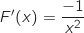Pour a. : donc c'est pas bon.
Pour b. :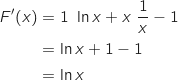
Donc la bonne réponse est la réponse b.
3. La valeur exacte de l'intégrale
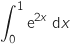est égale à :
On calcule l'intégrale, pour cela on remarque qu'une primitive de la fonction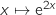 
est 
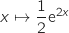et donc :
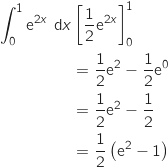Donc la bonne réponse est la réponse d.
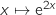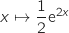4. Si une variable aléatoire est et donc :
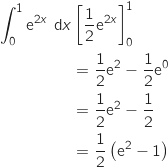Donc la bonne réponse est la réponse d.
suit la loi normale 
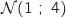, alors une valeur approchée au centième de 
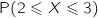est :
En utilisant la calculette on trouve directement :
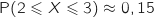Donc la bonne réponse est la réponse a.
Attention il faut bien prendre garde à entrer dans la calculette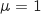 
et surtout 
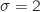(et non 4 qui représente 
).
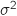5. Dans une commune comptant plus de 10 0000 habitants, un institut réalise un sondage auprès de la population. Sur 100 personnes interrogées, 55 affirment être satisfaites de leur maire.
L'intervalle de confiance au niveau de confiance 0,95 permettant de connaître la cote de popularité du maire est :
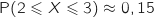Donc la bonne réponse est la réponse a.
Attention il faut bien prendre garde à entrer dans la calculette 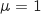et surtout 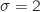(et non 4 qui représente ).
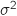On utilise la formule du cours pour l'intervalle de confiance à 95 % :
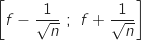
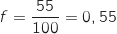et 
.
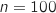Le rayon de l'intervalle est donc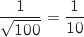 
et l'intervalle de confiance est :
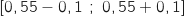soit 
.
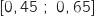Donc la bonne réponse est la réponse c.
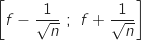
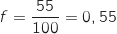et .
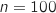Le rayon de l'intervalle est donc 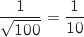et l'intervalle de confiance est :
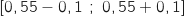soit .
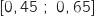Donc la bonne réponse est la réponse c.
