Sujet et corrigé de l'exercice 2 du bac ES de maths de mai 2013 au Liban
Cacher les corrigés
Partie A
On considère la suite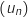 définie par
définie par 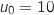 et pour tout entier naturel
et pour tout entier naturel  ,
,
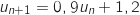
1. On considère la suite
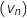 définie pour tout entier naturel
définie pour tout entier naturel  par
par 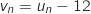 .
a. Démontrer que la suite
.
a. Démontrer que la suite 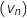 est une suite géométrique dont on précisera le premier terme et la raison.
est une suite géométrique dont on précisera le premier terme et la raison.
Pour tout entier naturel  on a :
on a :
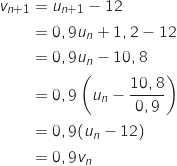 Donc la suite
Donc la suite  est une suite géométrique de raison 0,9 et de premier terme :
est une suite géométrique de raison 0,9 et de premier terme :
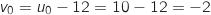 .
.
b. Exprimer  on a :
on a :
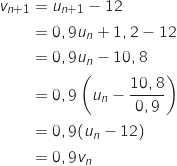 Donc la suite
Donc la suite  est une suite géométrique de raison 0,9 et de premier terme :
est une suite géométrique de raison 0,9 et de premier terme :
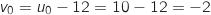 .
.
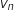 en fonction de
en fonction de  .
.
La formule explicite de la suite géométrique déterminée à la question précédente est :
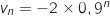
c. En déduire que pour tout entier naturel 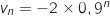
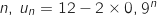 .
.
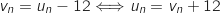 On remplace
On remplace 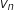 par sa formule explicite ce qui donne :
par sa formule explicite ce qui donne :
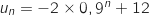
2. Déterminer la limite de la suite
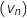 et en déduire celle de la suite
et en déduire celle de la suite 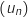 .
.
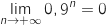 car
car 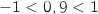 .
Par produit,
.
Par produit, 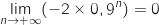 .
En ajoutant 12 ; on obtient
.
En ajoutant 12 ; on obtient 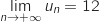 .
.
Partie B
En 2012, la ville de Bellecité compte 10 milliers d'habitants. Les études démographiques sur les dernières années ont montré que chaque année :- 10 % des habitants de la ville meurent ou déménagent dans une autre ville ;
- 1 200 personnes naissent ou emménagent dans cette ville.
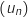 où
où 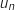 désigne le nombre de milliers d'habitants de la ville de Bellecité l'année
désigne le nombre de milliers d'habitants de la ville de Bellecité l'année 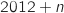 .
.
- D'une année à l'autre 10 % des habitants « diparaissent » donc il en reste 90 % soit
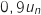 ;
;
- il y a 1 200 nouveaux habitants soit 1,2 milliers.
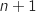 est égal à :
est égal à : 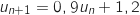 .
En outre on sait qu'en 2012 la ville compte 10 milliers d'habitants et que
.
En outre on sait qu'en 2012 la ville compte 10 milliers d'habitants et que 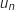 désigne le nombre d'habitants l'année
désigne le nombre d'habitants l'année 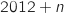 donc
donc 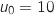 .
Ainsi la suite
.
Ainsi la suite  correspond bien à celle donnée dans la partie A.
correspond bien à celle donnée dans la partie A.
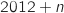 .
.

On complète la boucle pour avec la relation de récurrence permettant de calculer les termes successifs de la suite :

3.a. Résoudre l'inéquation 
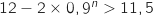 .
.
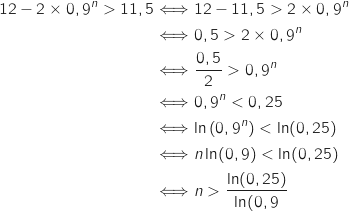 On remarquera qu'on a changé le sens de la dernière inégalité quand on a divisé par
On remarquera qu'on a changé le sens de la dernière inégalité quand on a divisé par 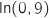 car
car 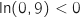 puisque
puisque 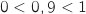 .
.
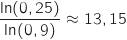 et comme
et comme  est un entier on conclut que l'ensemble des solutions de l'inéquation
est constitué des nombres entiers supérieurs ou égaux à 14.
est un entier on conclut que l'ensemble des solutions de l'inéquation
est constitué des nombres entiers supérieurs ou égaux à 14.
On a résolu 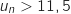 , on a donc déterminé le rang de l'année à partir de laquelle la population de Bellecité dépasse 11,5 milliers d'habitants et on
a trouvé que c'est à partir de
, on a donc déterminé le rang de l'année à partir de laquelle la population de Bellecité dépasse 11,5 milliers d'habitants et on
a trouvé que c'est à partir de 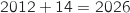 .
.
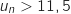 , on a donc déterminé le rang de l'année à partir de laquelle la population de Bellecité dépasse 11,5 milliers d'habitants et on
a trouvé que c'est à partir de
, on a donc déterminé le rang de l'année à partir de laquelle la population de Bellecité dépasse 11,5 milliers d'habitants et on
a trouvé que c'est à partir de 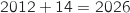 .
.
