Sujet et corrigé de l'exercice 3 du bac ES de maths de mai 2013 au Liban
Cacher les corrigés
Partie A
On considère la fonction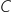 définie sur l'intervalle
définie sur l'intervalle 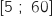 par :
par :
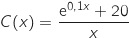
1. On désigne par
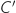 la dérivée de la fonction
la dérivée de la fonction 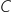 .
Montrer que, pour tout
.
Montrer que, pour tout 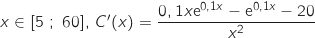 .
.
On peut écrire 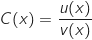 avec :
avec :
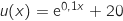 ;
; 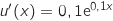
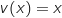 ;
; 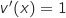 Donc
Donc 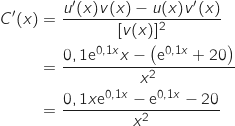
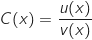 avec :
avec :
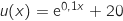 ;
; 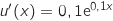
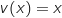 ;
; 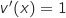 Donc
Donc 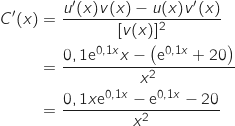
2. On considère la fonction
 définie sur
définie sur 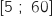 par
par
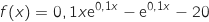
 est strictement croissante sur
est strictement croissante sur 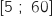 .
.
On étudie les variations de  en calculant la dérivée de la fonction
en calculant la dérivée de la fonction  :
:
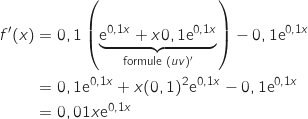 Pour tout
Pour tout 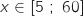 ;
; 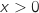 et
et 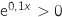 donc
donc 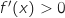 ce qui entraîne que
ce qui entraîne que  est strictement croissante sur l'intervalle considéré et on a le tableau de variations :
est strictement croissante sur l'intervalle considéré et on a le tableau de variations :
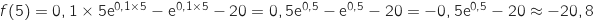
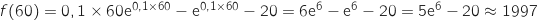
b. Montrer que l'équation  en calculant la dérivée de la fonction
en calculant la dérivée de la fonction  :
:
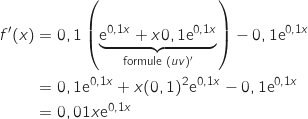 Pour tout
Pour tout 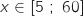 ;
; 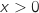 et
et 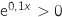 donc
donc 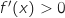 ce qui entraîne que
ce qui entraîne que  est strictement croissante sur l'intervalle considéré et on a le tableau de variations :
est strictement croissante sur l'intervalle considéré et on a le tableau de variations :

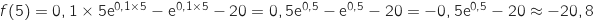
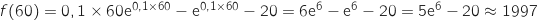
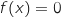 possède une unique solution
possède une unique solution  dans
dans 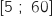 .
.
La fonction  est continue et strictement croissante sur
est continue et strictement croissante sur 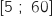 avec :
avec : 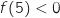 et
et 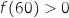 , donc d'après
le théorème de la valeur intermédiaire l'équation
, donc d'après
le théorème de la valeur intermédiaire l'équation 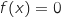 admet une unique solution
admet une unique solution  dans
dans 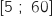 .
.
c. Donner un encadrement à l'unité de  est continue et strictement croissante sur
est continue et strictement croissante sur 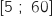 avec :
avec : 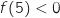 et
et 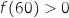 , donc d'après
le théorème de la valeur intermédiaire l'équation
, donc d'après
le théorème de la valeur intermédiaire l'équation 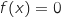 admet une unique solution
admet une unique solution  dans
dans 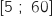 .
.
 .
.
En utilisant la calculette on trouve : 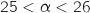
d. En déduire le tableau de signes de 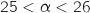
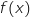 sur
sur 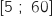 .
.
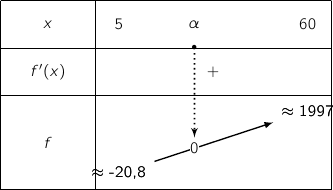
D'après ce qui précède on obtient facilement le tableau de signes :

3. En déduire le tableau de variations de 
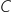 sur
sur 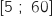 .
.
On remarque que pour tout 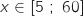 ,
, 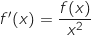 ; donc le signe de
; donc le signe de
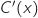 est le même que celui de
est le même que celui de 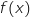 et on a le tableau de variations :
et on a le tableau de variations :
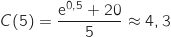
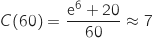 Pour
Pour 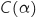 on est bien embêté car on a seulement l'encadrement
on est bien embêté car on a seulement l'encadrement 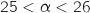 , mais en calculant
, mais en calculant 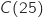 et
et 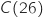 on remarque que
on remarque que
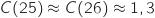 , donc on peut prendre
, donc on peut prendre 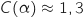 .
.
4. En utilisant le tableau de variations précédent, déterminer le nombre de solutions des équations suivantes :
a. 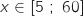 ,
, 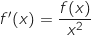 ; donc le signe de
; donc le signe de
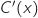 est le même que celui de
est le même que celui de 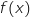 et on a le tableau de variations :
et on a le tableau de variations :

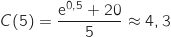
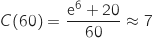 Pour
Pour 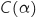 on est bien embêté car on a seulement l'encadrement
on est bien embêté car on a seulement l'encadrement 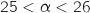 , mais en calculant
, mais en calculant 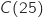 et
et 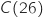 on remarque que
on remarque que
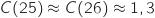 , donc on peut prendre
, donc on peut prendre 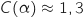 .
.
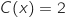 .
b.
.
b. 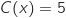 .
.
Par lecture du tableau de variations précédent :
-
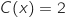 posséde deux solutions : une dans
posséde deux solutions : une dans 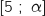 et l'autre dans
et l'autre dans 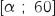 ;
;
-
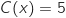 posséde une seule solution dans
posséde une seule solution dans 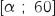 .
.
Partie B
Une entreprise fabrique chaque mois vélos de course, avec
vélos de course, avec  appartenant à l'intervalle
appartenant à l'intervalle 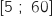 .
Le coût moyen de fabrication, exprimé en milliers d'euros, pour une production de
.
Le coût moyen de fabrication, exprimé en milliers d'euros, pour une production de  vélos de course, est donné par la fonction
vélos de course, est donné par la fonction 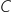 définie dans la partie A.
Déterminer le nombre de vélos à produire pour que le coût de fabrication moyen soit minimal.
définie dans la partie A.
Déterminer le nombre de vélos à produire pour que le coût de fabrication moyen soit minimal.
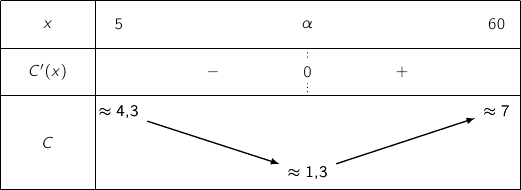
D'après l'étude précédente sur 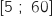 le minimum de la fonction
le minimum de la fonction 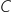 est obtenu en
est obtenu en  , donc il faut produire 25 ou 26 vélos.
Pour trancher entre les deux possibilités on compare
, donc il faut produire 25 ou 26 vélos.
Pour trancher entre les deux possibilités on compare 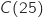 et
et 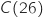 :
:
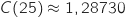 et
et 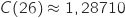 Donc pour avoir le coût moyen minimum l'entreprise doit fabriquer 26 vélos.
Donc pour avoir le coût moyen minimum l'entreprise doit fabriquer 26 vélos.
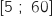 le minimum de la fonction
le minimum de la fonction  est obtenu en
est obtenu en  , donc il faut produire 25 ou 26 vélos.
Pour trancher entre les deux possibilités on compare
, donc il faut produire 25 ou 26 vélos.
Pour trancher entre les deux possibilités on compare 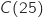 et
et 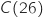 :
:
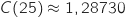 et
et 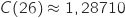 Donc pour avoir le coût moyen minimum l'entreprise doit fabriquer 26 vélos.
Donc pour avoir le coût moyen minimum l'entreprise doit fabriquer 26 vélos.
