Sujet et corrigé de l'exercice 4 du bac ES de maths de mai 2013 au Liban
Cacher les corrigés
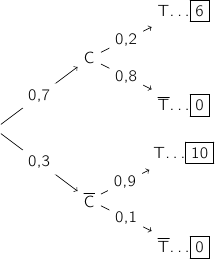
Un propriétaire d'une salle louant des terrains de squash s'interroge sur le taux d'occupation de ses terrains. Sachant que la location d'un terrain dure une heure, il a classé les heures en deux catégories : les heures pleines (soir et week-end) et les heures creuses (le reste de la semaine). Dans le cadre de cette répartition, 70 % des heures sont creuses. Une étude statistique sur une semaine lui a permis de s'apercevoir que :- lorsque l'heure est creuse, 20 % des terrains sont occupés ;
- lorsque l'heure est pleine, 90 % des terrains sont occupés.
- C : « l'heure est creuse »
- T : « le terrain est occupé »
1. Représenter cette situation par un arbre de probabilités.
En utilisant la formule des probabilités composées (multiplication sur les branches de l'arbre) :
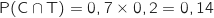
3. Déterminer la probabilité que le terrain soit occupé.
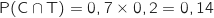
Les événements C et 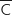 forment une partition de l'univers donc d'après la formule des probabilités totales :
forment une partition de l'univers donc d'après la formule des probabilités totales :
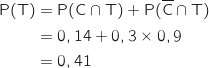
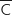 forment une partition de l'univers donc d'après la formule des probabilités totales :
forment une partition de l'univers donc d'après la formule des probabilités totales :
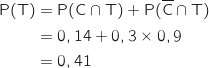
4. Montrer que la probabilité que l'heure soit pleine, sachant que le terrain est occupé, est égale à
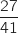 .
.
La relation de définition de la probabilité conditionnelle donne :
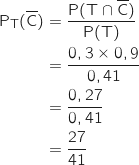
Dans le but d'inciter ses clients à venir hors des heures de grande fréquentation, le propriétaire a instauré, pour la location d'un terrain, des tarifs différenciés :
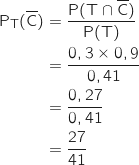
- 10 € pour une heure pleine,
- 6 € pour une heure creuse.
 la variable aléatoire qui prend pour valeur la recette en euros obtenue grâce à la location d'un terrain de la salle, choisi au hasard. Ainsi,
la variable aléatoire qui prend pour valeur la recette en euros obtenue grâce à la location d'un terrain de la salle, choisi au hasard. Ainsi,  prend 3 valeurs :
prend 3 valeurs :
- 10 lorsque le terrain est occupé et loué en heure pleine,
- 6 lorsque le terrain est occupé et loué en heure creuse,
- 0 lorsque le terrain n'est pas occupé.
 .
.
En utilisant les résultats précédents et l'arbre on a le tableau suivant :
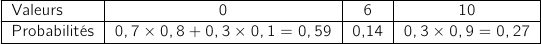
6. Déterminer l'espérance de 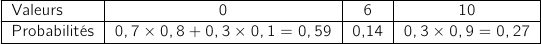
 .
.
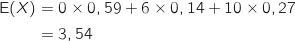
La question précédente indique qu'en moyenne un terrain rapporte 3,54 € par heure d'ouverture de la salle. Dans la situation indiquée le
propriétaire peut donc espérer gagner 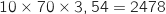 € par semaine.
€ par semaine.
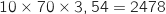 € par semaine.
€ par semaine.
