Sujet et corrigé de l'exercice 4 du bac ES de maths de mai 2014 au Liban
Cacher les corrigés
Partie A
On considère la fonction définie sur l'intervalle par
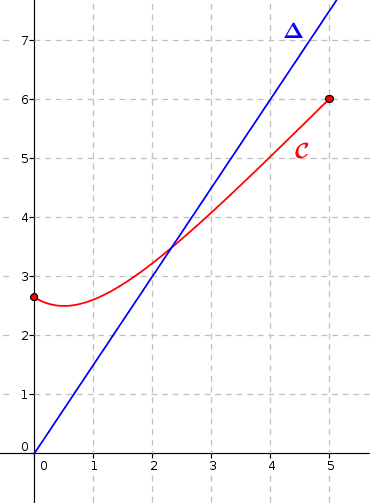
On a représenté ci-dessous, dans un plan muni d'un repère orthonormé :
la courbe représentative de la fonction ,
la droite d'équation .
1.a. Vérifier que pour tout appartenant à l'intervalle , on a :
où désigne la fonction dérivée de .
Pour tout on a :
avec :
;
Donc .
b. Résoudre dans l'intervalle l'équation .
c. Etudier le signe de sur l'intervalle .
De la même façon qu'on a résolu l'équation ci-avant :
et on a aussi : .
d. Dresser le tableau de variations de la fonction sur l'intervalle .
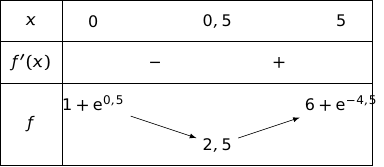
;
;
2. On note l'abscisse du point d'intersection de et .
a. Donner, par lecture graphique, un encadrement de à 0,5 près.
On a .
b. Résoudre graphiquement sur l'intervalle l'inéquation .
Graphiquement les solutions de l'inéquation proposée correspond à l'ensemble des abscisses des points pour lesquels la droite est située au dessus de la courbe .
Donc, sur , .
Partie B : Application
Une entreprise fabrique des cartes à puces électroniques à l'aide d'une machine.
La fonction , définie dans la partie A, représente le coût d'utilisation de la machine en fonction de la quantité de cartes produites, lorsque est exprimé en centaines de cartes et en centaines d'euros.
1.a. Déduire de la partie A, le nombre de cartes à produire pour avoir un coût minimal d'utilisation de la machine.
L'étude des variations de a mis en évidence un minimum pour .
Pour avoir le coût minimal d'utilisation il faut produire 50 cartes.
b. Chaque carte fabriquée par la machine est vendue 1,50 €.
La recette perçue pour la vente de centaines de cartes vaut donc centaines d'euros.
Vérifier que le bénéfice obtenu en centaines d'euros, par la vente de centaines de cartes est donné par :
Pour obtenir le bénéfice on retranche le coût de la recette soit :
2.a. Montrer que la fonction est strictement croissante sur l'intervalle .
Pour tout , on a :
or pour , , et en ajoutant 0,5 on a encore , ce qui montre que est strictement croissante sur l'intervalle considéré.
b. Montrer que, sur l'intervalle , l'équation admet une unique solution comprise entre 2,32 et 2,33.
La fonction est continue et strictement croissante sur .
On a de plus :
donc et d'après le théorème de la valeur intermédiaire l'équation a une unique solution dans .
On remarque de plus que (négatif) et (positif) donc la solution est comprise entre 2,32 et 2,33.
3. On dira que l'entreprise réalise un bénéfice lorsque .
Indiquer la quantité minimale qui doit figurer sur le carnet de commandes de l'entreprise pour que celle-ci puisse réaliser un bénéfice.
D'après l'étude précédente, la fonction est croissante et s'annule pour (valeur approchée par excès), donc l'entreprise réalise un bénéfice à partir de 233 cartes à puces sur son carnet de commandes.
