Corrigé de l'exercice 3 de maths du bac ES de juin 2012 en métropole
Cacher les corrigés
Cet exercice est un QCM (questionnaire à choix multiples). Pour chacune des questions posées, une seule des quatre réponses est exacte. Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse choisie. Aucune justification n'est demandée. Une réponse exacte rapporte 1 point, une réponse fausse ou l'absence de réponse ne rapporte ni n'enlève aucun point.
On a représenté ci-dessous, dans le plan muni d'un repère orthogonal, la courbe représentative
 d'une fonction
d'une fonction  définie et dérivable sur l'intervalle
définie et dérivable sur l'intervalle 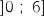 .
Le point A
.
Le point A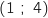 appartient à la courbe
appartient à la courbe  .
La tangente en A à la courbe
.
La tangente en A à la courbe  est parallèle à l'axe des abscisses.
On note
est parallèle à l'axe des abscisses.
On note 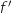 la fonction dérivée de la fonction
la fonction dérivée de la fonction  .
.
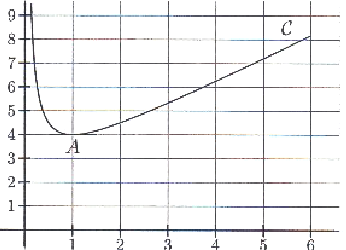
 en 1 est égal à :
en 1 est égal à :

La bonne réponse est la réponse b.
En effet la tangente au point d'abscisse 1 est « horizontale », donc le nombre dérivé est nul.
2. Sur l'intervalle
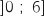 , l'inéquation
, l'inéquation 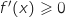 admet comme ensemble de solutions :
admet comme ensemble de solutions :

La bonne réponse est la réponse c.
En effet la fonction est croissante sur 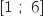 ce qui équivaut à
ce qui équivaut à 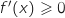 .
.
3. On pose 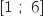 ce qui équivaut à
ce qui équivaut à 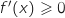 .
.
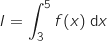 . On peut affirmer que :
. On peut affirmer que :

La bonne réponse est la réponse a.
En comptant les carreaux, l'aire sous la courbe est approximativement entre 12 et 13 u.a.
4. On appelle  une primitive de la fonction
une primitive de la fonction  sur l'intervalle
sur l'intervalle 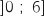 .
L'expression de F peut être :
.
L'expression de F peut être :
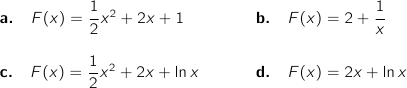
La bonne réponse est la réponse c.
Pour le voir, il suffit de dériver chacune des propositions et de regarder si 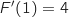 .
Il se trouve que l'on a cela que pour la proposition c.
.
Il se trouve que l'on a cela que pour la proposition c.
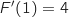 .
Il se trouve que l'on a cela que pour la proposition c.
.
Il se trouve que l'on a cela que pour la proposition c.
