Corrigé de l'exercice 4 de maths du bac ES de juin 2012 en métropole
Cacher les corrigés
Le bénéfice en milliers d'euros que réalise une entreprise lorsqu'elle fabrique et vend x centaines d'objets (pour x compris entre 0 et 6) est donné par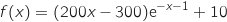
 sur l'intervalle
sur l'intervalle 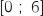 .
.
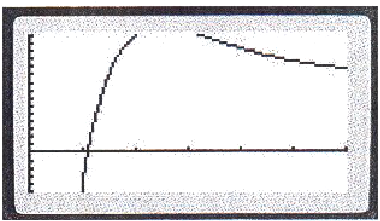
Partie A : objectif « réaliser un bénéfice maximal »
L'écran ne permet pas à Alix de déterminer le bénéfice maximal. Il décide donc d'étudier la fonction sur l'intervalle
sur l'intervalle 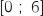 .
On admet que cette fonction est dérivable sur l'intervalle
.
On admet que cette fonction est dérivable sur l'intervalle 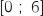 . On désigne par
. On désigne par 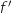 la fonction dérivée de la fonction
la fonction dérivée de la fonction  .
1. Etablir que, pour tout nombre réel
.
1. Etablir que, pour tout nombre réel  de l'intervalle
de l'intervalle 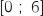 ,
,
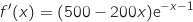
On a 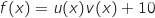 avec :
avec :
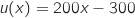
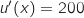
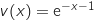
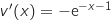 (ne pas oublier le
(ne pas oublier le  , qui provient de la dérivée de la composée).
, qui provient de la dérivée de la composée).
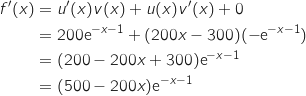
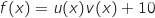 avec :
avec :
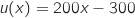
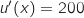
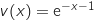
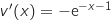 (ne pas oublier le
(ne pas oublier le  , qui provient de la dérivée de la composée).
, qui provient de la dérivée de la composée).
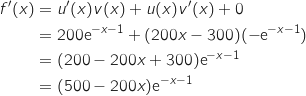
2. Dresser le tableau de variation de la fonction
 sur l'intervalle
sur l'intervalle 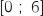 .
.
Pour tout 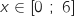 ,
, 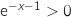 , donc le signe de
, donc le signe de  est le même que celui du binôme du premier degré
est le même que celui du binôme du premier degré 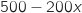 .
Ce binôme s'annule pour
.
Ce binôme s'annule pour 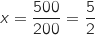 et on a le tableau de variations :
et on a le tableau de variations :
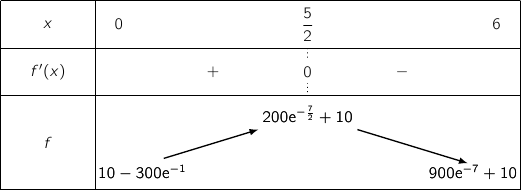
3. En déduire le nombre d'objets à vendre pour réaliser un bénéfice maximal.
Quel est ce bénéfice maximal en euros ? (Donner la réponse arrondie à l'euro).
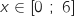 ,
, 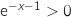 , donc le signe de
, donc le signe de  est le même que celui du binôme du premier degré
est le même que celui du binôme du premier degré 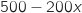 .
Ce binôme s'annule pour
.
Ce binôme s'annule pour 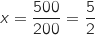 et on a le tableau de variations :
et on a le tableau de variations :

Par observation du tableau de variations précédent, on peut dire que le bénéfice maximal est obtenu pour 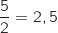 centaines soit 250 objets vendus.
Le bénéfice obtenus en milliers d'euros est alors :
centaines soit 250 objets vendus.
Le bénéfice obtenus en milliers d'euros est alors :
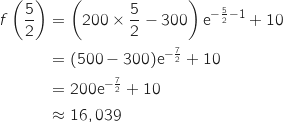 Donc le bénéfice est d'environ 16 039 euros.
Donc le bénéfice est d'environ 16 039 euros.
4. Proposer un réglage de la fenêtre graphique permettant de visualiser le maximum de la fonction 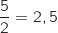 centaines soit 250 objets vendus.
Le bénéfice obtenus en milliers d'euros est alors :
centaines soit 250 objets vendus.
Le bénéfice obtenus en milliers d'euros est alors :
 Donc le bénéfice est d'environ 16 039 euros.
Donc le bénéfice est d'environ 16 039 euros.
 .
.
xmin=0 xmax=6 ymin=0 ymax=17
Partie B : objectif « ne pas vendre à perte »
1. Au vu du graphique obtenu par Alix, à partir de combien d'objets l'entreprise ne vend-elle pas à perte ?
Par lecture graphique on estime que l'entreprise réalise un bénéfice positif à partir d'un peu plus d'une centaine d'objets vendus.
2. Démontrer que sur l'intervalle 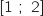 l'équation
l'équation 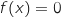 admet une unique solution notée
admet une unique solution notée  .
.
La fonction  est strictement croissante et continue sur l'intervalle
est strictement croissante et continue sur l'intervalle 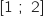 et de plus on a :
et de plus on a :
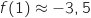 et
et 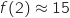 , donc
, donc 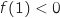 et
et 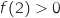 et d'après le théorème des valeurs intermédiaires on peut dire que l'équation
et d'après le théorème des valeurs intermédiaires on peut dire que l'équation 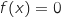 admet une unique solution
dans l'intervalle
admet une unique solution
dans l'intervalle 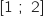 .
.
3. Donner une valeur approchée de  est strictement croissante et continue sur l'intervalle
est strictement croissante et continue sur l'intervalle 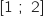 et de plus on a :
et de plus on a :
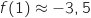 et
et 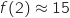 , donc
, donc 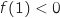 et
et 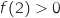 et d'après le théorème des valeurs intermédiaires on peut dire que l'équation
et d'après le théorème des valeurs intermédiaires on peut dire que l'équation 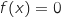 admet une unique solution
dans l'intervalle
admet une unique solution
dans l'intervalle 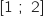 .
.
 à
à 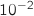 près.
près.
En utilisant la calculette on trouve 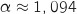 .
.
4. Préciser le nombre d'objets à partir duquel l'entreprise ne vend pas à perte.
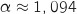 .
.
D'après ce qui précède on peut dire que l'entreprise ne vend pas à perte à partir de 110 objets (la valeur de seuil  est telle que
est telle que 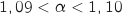 ).
).
 est telle que
est telle que 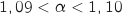 ).
).
