Sujet et corrigé de l'exercice 4 du bac ES de maths de mars 2014 en Nouvelle-Calédonie
Cacher les corrigés
Soit la fonction définie sur l'intervalle par
soit sa fonction dérivée et soit sa fonction dérivée seconde.
1. Montrer que, pour tout nombre réel appartenant à l'intervalle et .
avec
; et ;
avec ; et ;
2. Etudier les variations de la fonction sur l'intervalle .
On cherche le signe de sur .
Pour tout ,
Le signe de est le même que celui de .
Or , donc pour tout , (et ne s'annule que pour ) donc est strictement décroissante sur l'intervalle considéré.
3. Justifier que l'équation admet une unique solution dans l'intervalle .
Montrer que : .
Tableau de variations
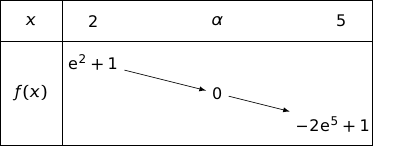
;
est continue et strictement décroissante sur
et
or donc d'après le théorème de la valeur intermédiaire il existe un unique tel que .
et , du coup , donc .
4.a. Soit T la tangente à la courbe représentative de la fonction au point d'abscisse 3.
Montrer que T a pour équation .
On sait que l'équation réduite de T est :
où et
donc soit
b. Déterminer les coordonnées du point d'intersection de la droite T et de l'axe des abscisses.
On résout :
c. Etudier le signe de sur l'intervalle et en déduire la convexité ou la concavité de sur cet intervalle.
Pour tout ;
Le signe de est le même que celui de .
; donc pour tout , .
Donc la fonction est concave sur l'intervalle considéré.
d. En déduire que :
On a donc : .
est concave donc est placée en dessous de la tangente T.
En particulier :
le point de T d'abscisse est situé au dessus de l'axe des abscisses,
T coupe l'axe des abscisses en .
Un dessin pour comprendre :
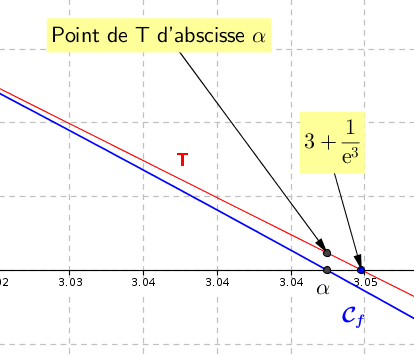
5. On considère l'algorithme suivant :
| Variables : | ,, et sont des nombres réels |
| Initialisation : | Affecter à la valeur 3 |
| Affecter à la valeur 3,05 | |
| Entrée : | Saisir |
| Traitement : | TANT QUE |
| Affecter à la valeur | |
| SI | |
| ALORS Affecter à la valeur | |
| SINON Affecter à la valeur | |
| FIN SI | |
| FIN TANT QUE | |
| Sortie : | Afficher |
| Afficher |
a. Faire fonctionner l'algorithme précédent avec en recopiant et complétant le tableau ci-dessous. On arrondira au millième les valeurs de .
| Initialisation | 3 | 3,05 | |||||
| Etape 1 | 0,05 | oui | 3,025 | 0,485 | oui | 3,025 | 3,05 |
| Etape 2 | |||||||
| Etape 3 |
| Initialisation | 3 | 3,05 | |||||
| Etape 1 | 0,05 | oui | 3,025 | 0,485 | oui | 3,025 | 3,05 |
| Etape 2 | 0,025 | oui | 3,0375 | 0,218 | oui | 3,0375 | 3,05 |
| Etape 3 | 0,0125 | oui | 3,04375 | 0,082 | oui | 3,04375 | 3,05 |
b. Interpréter les résultats trouvés pour et à la fin de l'étape 3.
C'est l'algorithme de dichotomie qui permet de trouver une valeur approchée de .
A la fin de l'étape 3, on obtient : , ce qui donne un encadrement de d'amplitude : .
