Sujet et corrigé de l'exercice de spécialité du bac ES de maths de mars 2014 en Nouvelle-Calédonie
Cacher les corrigés
On a observé l'évolution des inscriptions dans le club de gymnastique d'une ville.
Chaque année, 30 % des personnes inscrites au club de gymnastique l'année précédente renouvellent leur inscription au club.
De plus, chaque année, 10 % des habitants de la ville qui n'étaient pas inscrits au club l'année précédente s'y inscrivent.
On appelle le nombre d'années d'existence du club.
On note la proportion de la population de la ville inscrite au club de gymnastique lors de l'année et la proportion de la population qui n'y est pas inscrite.
La première année de fonctionnement du club (année « zéro »), 20 % des habitants de la ville se sont inscrits.
On note la matrice traduisant l'état probabiliste de l'année .
On a donc .
1. Traduire les données de l'énoncé par un graphe probabiliste.
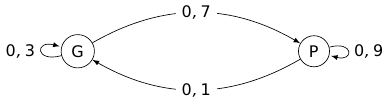
2. On nomme A la matrice de transition associée à cette situation, c'est-à-dire la matrice vérifiant : pour tout entier naturel , .
Donner la matrice A.
3. Déterminer et . Interpréter les résultats.
La deuxième année de fonctionnement, 14 % de la population est inscrite au club et 86 % non.
La troisième année de fonctionnement, 12,8 % de la population est inscrite au club et 87,2 % non.
4. Déterminer l'état probabiliste stable (on donnera les coefficients de la matrice ligne sous la forme de fractions irréductibles).
Comment peut-on interpréter ce résultat ?
On cherche E tel que soit :
ce qui donne le système :
On n'oublie pas que donc finalement on résout :
Donc l'état stable est
Au fil du temps la proportion de personnes inscrites au club va tendre et se stabiliser vers soit 12,5 % de la population de la ville.
