Corrigé de l'exercice 2 du bac ES de maths de juin 2012 en Polynésie
Cacher les corrigés
L'Etat du Wyoming, aux Etats-Unis, accueille chaque année près de 3,5 millions de touristes, notamment venus visiter les parcs nationaux de Yellowstone et de Grand Teton. 92 % de ces touristes visitent le parc de Yellowstone ; parmi ceux-là, 60 % visitent aussi le parc du Grand Teton. Enfin, 6 % des touristes se rendant au Wyoming ne visitent aucun des deux parcs. On interroge au hasard un touriste s'étant rendu au Wyoming ; on suppose que tous ces touristes ont la même probabilité d'être interrogés. On note Y l'événement : « le touriste a visité le parc de Yellowstone » ;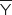 désigne l'événement contraire de Y.
On note G l'événement : « le touriste a visité le parc du Grand Teton » ;
désigne l'événement contraire de Y.
On note G l'événement : « le touriste a visité le parc du Grand Teton » ; 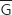 désigne l'événement contraire de G.
On note
désigne l'événement contraire de G.
On note 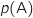 la probabilité d'un événement A et, si B est un événement de probabilité non nulle,
la probabilité d'un événement A et, si B est un événement de probabilité non nulle, 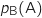 la probabilité de l'événement A sachant que l'événement B est réalisé.
Si nécessaire, les résultats seront arrondis à
la probabilité de l'événement A sachant que l'événement B est réalisé.
Si nécessaire, les résultats seront arrondis à 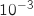 près.
près.
1. Que vaut
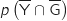 la probabilité de l'événement «
la probabilité de l'événement « 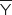 et
et 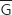 » ?
» ?
D'après l'énoncé 6 % des touristes ne visitent aucun des deux parcs donc :
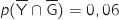
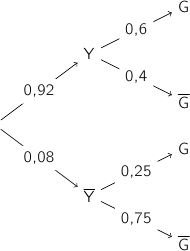
2. Construire un arbre pondéré décrivant la situation étudiée, en y indiquant les probabilités données par l'énoncé qui correspondent à certaines de ses branches.
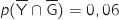
3. Calculer
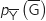 .
Interpréter ce résultat par une phrase.
.
Interpréter ce résultat par une phrase.
On utilise la formule :
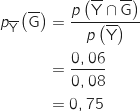 Parmi les touristes qui ne visitent pas Yellowstone 75 % ne visitent pas non plus Grand Teton.
On peut terminer de compléter l'arbre grâce à ce résultat.
Parmi les touristes qui ne visitent pas Yellowstone 75 % ne visitent pas non plus Grand Teton.
On peut terminer de compléter l'arbre grâce à ce résultat.
4. Montrer que 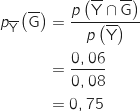 Parmi les touristes qui ne visitent pas Yellowstone 75 % ne visitent pas non plus Grand Teton.
On peut terminer de compléter l'arbre grâce à ce résultat.
Parmi les touristes qui ne visitent pas Yellowstone 75 % ne visitent pas non plus Grand Teton.
On peut terminer de compléter l'arbre grâce à ce résultat.
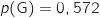 .
.
Les événements Y et 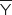 forment une partition de l'univers, donc d'après la formule des probabilités totales :
forment une partition de l'univers, donc d'après la formule des probabilités totales :
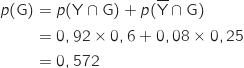
5. Un touriste a visité le parc du Grand Teton. Calculer la probabilité qu'il ait aussi visité le parc de Yellowstone (le résultat sera arrondi à 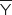 forment une partition de l'univers, donc d'après la formule des probabilités totales :
forment une partition de l'univers, donc d'après la formule des probabilités totales :
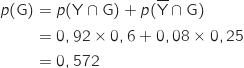
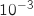 près).
près).
Il s'agit de calculer 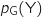 .
.
6. Le billet d'entrée pour le parc de Yellowstone est de 10 dollars, celui pour le parc du Grand Teton est de 7 dollars.
a. Recopier et compléter le tableau suivant donnant la loi de probabilité de la somme, en dollars, dépensée pour la visite des parcs
de Yellowstone et du Grand Teton par un touriste se rendant au Wyoming.
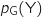 .
.

Les colonnes du tableau correspondent aux 4 possibilités mises en évidence dans l'arbre de probabilités. On obtient les probabilités en utilisant le principe
multiplicatif sur les branches de l'arbre.

b. Calculer l'espérance de cette loi et interpréter le résultat.

L'espérance de la loi précédente est :
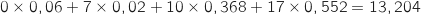 Donc en moyenne un touriste se rendant au Wyoming dépense 13,20 dollars pour vister les parcs.
Donc en moyenne un touriste se rendant au Wyoming dépense 13,20 dollars pour vister les parcs.
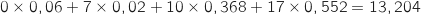 Donc en moyenne un touriste se rendant au Wyoming dépense 13,20 dollars pour vister les parcs.
Donc en moyenne un touriste se rendant au Wyoming dépense 13,20 dollars pour vister les parcs.
