Sujet et corrigé de l'exercice 1 du bac ES de maths de juin 2013 en Polynésie
Cacher les corrigés
Cet exercice est un questionnaire à choix multiples. Pour chaque question, une seule des quatre réponses proposées est correcte. Une réponse juste rapporte 1 point ; une réponse fausse ou l'absence de réponse ne rapporte ni n'enlève de point. Reporter sur la copie le numéro de la question ainsi que la réponse choisie. Aucune justification n'est demandée.
On considère la fonction
 définie sur
définie sur  par :
par :
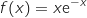
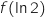 de
de 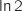 par
par  est égale à :
est égale à :

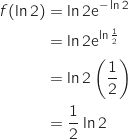 La bonne réponse est la réponse d.
La bonne réponse est la réponse d.
 est dérivable sur
est dérivable sur  et on note
et on note 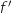 sa fonction dérivée.
Alors, pour tout nombre réel
sa fonction dérivée.
Alors, pour tout nombre réel  , on a :
, on a :


 se présente sous la forme d'un produit :
se présente sous la forme d'un produit : 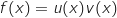 avec :
avec :
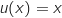 ;
; 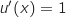
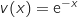 ;
; 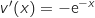 (attention à ne pas oublier le signe
(attention à ne pas oublier le signe  )
Donc
)
Donc 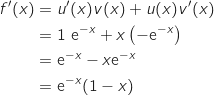 La bonne réponse est la réponse c.
La bonne réponse est la réponse c.
3. L'équation réduite de la tangente à la courbe de la fonction
 au point d'abscisse 0 est :
au point d'abscisse 0 est :

Cette équation s'écrit : 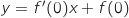 avec :
avec :
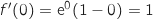 et
et 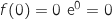 Donc cela donne
Donc cela donne 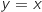 .
La bonne réponse est la réponse c.
.
La bonne réponse est la réponse c.
4. La fonction 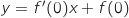 avec :
avec :
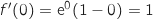 et
et 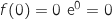 Donc cela donne
Donc cela donne 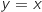 .
La bonne réponse est la réponse c.
.
La bonne réponse est la réponse c.
 est :
est :


On calcule la dérivée seconde en utilisant de nouveau la formule du produit :
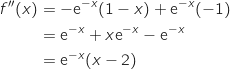 Donc le signe de la dérivée seconde est le même que celui de
Donc le signe de la dérivée seconde est le même que celui de 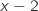 (car
(car 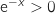 pour tout
pour tout  ) et on a le tableau de signes :
) et on a le tableau de signes :

On remarque que  ,
, 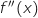 n'a pas un signe constant ce qui élimine les réponses c. et b.
Sur
n'a pas un signe constant ce qui élimine les réponses c. et b.
Sur  ,
, 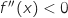 , donc la fonction est concave sur cet intervalle.
La bonne réponse est la réponse a.
Pour trouver cette réponse on peut aussi simplement regarder la courbe représentative de
, donc la fonction est concave sur cet intervalle.
La bonne réponse est la réponse a.
Pour trouver cette réponse on peut aussi simplement regarder la courbe représentative de  sur la calculette.
sur la calculette.
5. L'intégrale 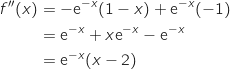 Donc le signe de la dérivée seconde est le même que celui de
Donc le signe de la dérivée seconde est le même que celui de 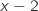 (car
(car 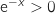 pour tout
pour tout  ) et on a le tableau de signes :
) et on a le tableau de signes :

 ,
, 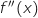 n'a pas un signe constant ce qui élimine les réponses c. et b.
Sur
n'a pas un signe constant ce qui élimine les réponses c. et b.
Sur  ,
, 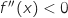 , donc la fonction est concave sur cet intervalle.
La bonne réponse est la réponse a.
Pour trouver cette réponse on peut aussi simplement regarder la courbe représentative de
, donc la fonction est concave sur cet intervalle.
La bonne réponse est la réponse a.
Pour trouver cette réponse on peut aussi simplement regarder la courbe représentative de  sur la calculette.
sur la calculette.
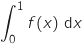 est égale à :
est égale à :

En TES on n'a pas les outils pour trouver une primitive de  . La réponse à cette question peut se faire en observant la courbe
de
. La réponse à cette question peut se faire en observant la courbe
de  ou en utilisant la fonctionnalité d'intégration de la calculette (pour ceux qui savent s'en servir).
L'observation de la courbe réprésentative de
ou en utilisant la fonctionnalité d'intégration de la calculette (pour ceux qui savent s'en servir).
L'observation de la courbe réprésentative de  montre que l'intégrale correspond à « l'aire sous la courbe » entre 0 et 1 et que cette aire
est bien inférieure à une unité d'aire. Cette observation permet d'éliminer les réponses b. et d. En outre on élimine a. car
montre que l'intégrale correspond à « l'aire sous la courbe » entre 0 et 1 et que cette aire
est bien inférieure à une unité d'aire. Cette observation permet d'éliminer les réponses b. et d. En outre on élimine a. car 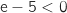 .
Du coup la bonne réponse est la réponse c.
.
Du coup la bonne réponse est la réponse c.
 . La réponse à cette question peut se faire en observant la courbe
de
. La réponse à cette question peut se faire en observant la courbe
de  ou en utilisant la fonctionnalité d'intégration de la calculette (pour ceux qui savent s'en servir).
L'observation de la courbe réprésentative de
ou en utilisant la fonctionnalité d'intégration de la calculette (pour ceux qui savent s'en servir).
L'observation de la courbe réprésentative de  montre que l'intégrale correspond à « l'aire sous la courbe » entre 0 et 1 et que cette aire
est bien inférieure à une unité d'aire. Cette observation permet d'éliminer les réponses b. et d. En outre on élimine a. car
montre que l'intégrale correspond à « l'aire sous la courbe » entre 0 et 1 et que cette aire
est bien inférieure à une unité d'aire. Cette observation permet d'éliminer les réponses b. et d. En outre on élimine a. car 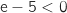 .
Du coup la bonne réponse est la réponse c.
.
Du coup la bonne réponse est la réponse c.
