Sujet et corrigé de l'exercice 2 du bac ES de maths de juin 2013 en Polynésie
Cacher les corrigés
Une agence de voyage propose des formules week-end à Londres au départ de Paris pour lesquelles le transport et l'hôtel sont compris. Les clients doivent choisir entre les deux formules : « avion + hôtel » ou « train + hôtel » et peuvent compléter ou non leur formule par une option « visites guidées ».
Une étude a produit les données suivantes :
- 40 % des clients optent pour la formule « avion + hôtel » et les autres pour la formule « train + hôtel » ;
- parmi les clients ayant choisi la formule « train + hôtel », 50 % choisissent aussi l'option « visites guidées » ;
- 12 % des clients ont choisi la formule « avion + hôtel » et l'option « visites guidées ».
On nous dit que 12 % des clients ont choisi la formule « avion + hôtel » et l'option « visites guidées » donc 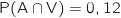 .
.
b) Calculer la probabilité 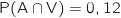 .
.
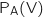 .
.
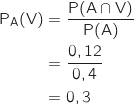
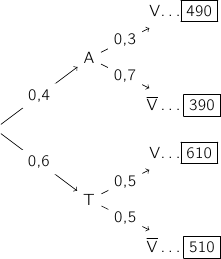
2. a) Montrer que la probabilité pour que le client interrogé ait choisi l'option « visites guidées » est égale à 0,42.
Les événements A et T forment une partition de l'univers donc d'après la formule des probabilités totales :
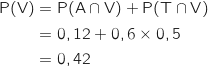
b) Calculer la probabilité pour que le client interrogé ait pris l'avion sachant qu'il n'a pas choisi l'option « visites guidées ». Arrondir le résultat au millième.
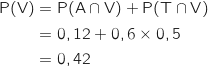
- Formule « avion + hôtel » : 390 €
- Formule « train + hôtel » : 510 €
- Formule « visites guidées » : 100 €
Soit  la variable aléatoire qui donne le prix du voyage pour une personne. La loi de X est la suivante :
la variable aléatoire qui donne le prix du voyage pour une personne. La loi de X est la suivante :

L'espérance de  vaut :
E
vaut :
E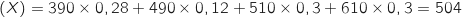 Donc pour 50 clients, l'agence peut espérer obtenir un chiffre d'affaire de
Donc pour 50 clients, l'agence peut espérer obtenir un chiffre d'affaire de 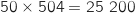 €.
€.
 la variable aléatoire qui donne le prix du voyage pour une personne. La loi de X est la suivante :
la variable aléatoire qui donne le prix du voyage pour une personne. La loi de X est la suivante :

 vaut :
E
vaut :
E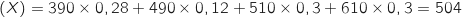 Donc pour 50 clients, l'agence peut espérer obtenir un chiffre d'affaire de
Donc pour 50 clients, l'agence peut espérer obtenir un chiffre d'affaire de 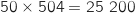 €.
€.
