Sujet et corrigé de l'exercice 3 du bac ES de maths de juin 2013 en Polynésie
Cacher les corrigés
La production des perles de culture de Tahiti est une activité économique importante pour la Polynésie Française. Les montants réalisés à l'exportation des produits perliers de 2008 à 2011 sont donnés dans le tableau suivant, en milliers d'euros :
1. Montrer que le taux d'évolution annuel moyen des montants à l'exportation des produits perliers de Polynésie entre 2008 et 2011 est
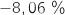arrondi au centième.
Le coefficient multiplicateur associé à l'évolution globale sur les 3 années vaut :
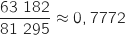Pour trouver le coefficient multiplicateur associé à l'évolution moyenne annuelle on élève le résultat précédent à la puissance 
(ou racine cubique) ce qui donne :
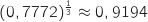Le coefficient multiplicateur obtenu correspond à une évolution de 
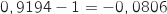soit une baisse de 8,06 %.
On admet pour la suite de l'exercice, que la production continuera à baisser de 8 % par an à partir de 2011.
2. On considère l'algorithme suivant :
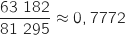Pour trouver le coefficient multiplicateur associé à l'évolution moyenne annuelle on élève le résultat précédent à la puissance (ou racine cubique) ce qui donne :
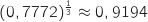Le coefficient multiplicateur obtenu correspond à une évolution de 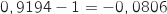soit une baisse de 8,06 %.
Si on saisit P=50 000 en entrée, qu'obtient-on en sortie par cet algorithme ?
Interpréter ce résultat dans le contexte de la production de perles.
En initialisation la variable U prend la valeur des produits perliers en 2011. Ensuite l'algorithme applique à U des baisses successives de 8 %
jusqu'à ce que U devienne inférieur ou égal à P soit 50 000. La variable N compte les baisses ainsi appliquées.
On sort ainsi de la boucle Tant que avec N
3, la dernière instruction de traitement ajoute 2011 et en sortie 2014 s'affiche.
Cela signifie que la valeur brute des produits perliers tombe en dessous de 50 000 milliers d'euros à partir de 2014.
3, la dernière instruction de traitement ajoute 2011 et en sortie 2014 s'affiche.
Cela signifie que la valeur brute des produits perliers tombe en dessous de 50 000 milliers d'euros à partir de 2014.
3. Pour prévoir les montants réalisés à l'exportation des perles de Tahiti, on modélise la situation par une suite
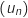. On note 
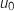le montant en 2011, en milliers d'euros, et 
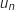le montant en 
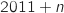, en milliers
d'euros. On a donc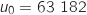 
et on suppose que la valeur baisse tous les ans de 8 %.
a. Montrer que 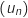est une suite géométrique dont on précisera la raison.
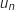désigne le montant l'année 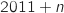, ce montant subi une baisse annuelle de 8 % ce qui revient à multiplier 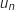par 0,92 pour obtenir le montant
de l'année suivante, on a donc la relation :
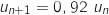, c'est la relation de récurrence d'une suite géométrique de raison 0,92.
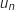, en fonction de .
La formule explicite de la suite géométrique ainsi considérée est :
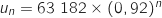
c. Avec ce modèle, quel montant peut-on prévoir pour l'exportation des produits perliers de Polynésie Française en 2016 ?
On arrondira le résultat au millier d'euros.
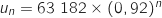
Le rang de l'année 2016 est 
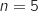(car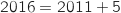 
). On remplace donc par 5
dans la formule explicite de la suite ce qui donne :
.
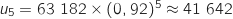Donc en 2016, on peut prévoir un montant de 40 983 €.
4. Calculer le montant cumulé des produits perliers exportés que l'on peut prévoir avec ce modèle à partir de 2011 (comprise) jusqu'à 2020 (comprise).
On donnera une valeur approchée au millier d'euros.
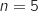de l'année 2016 est (car 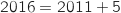). On remplace donc par 5
dans la formule explicite de la suite ce qui donne :
.
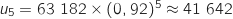Donc en 2016, on peut prévoir un montant de 40 983 €.
Il s'agit de calculer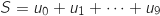 
.
Pour cela on utilise la formule de la somme des termes consécutifs d'une suite géométrique :
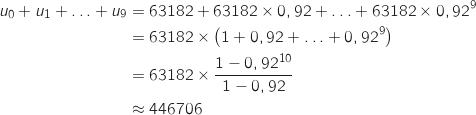Donc le montant cumulé entre 2011 et 2020 est d'environ 446 706 €.
.
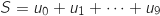Pour cela on utilise la formule de la somme des termes consécutifs d'une suite géométrique :
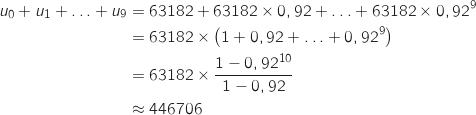Donc le montant cumulé entre 2011 et 2020 est d'environ 446 706 €.
