Sujet et corrigé de l'exercice 4 du bac ES de maths de juin 2013 en Polynésie
Cacher les corrigés
On s'intéresse à une espèce de poissons présente dans deux zones différentes (zone 1 et zone 2) de la planète.
A . Etude de la zone 1
On note
la variable aléatoire qui à chaque poisson observé dans la zone 1 associe sa taille en cm.
Une étude statistique sur ces poissons de la zone 1 a montré que la variable aléatoire suit une loi normale de moyenne 
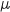et
d'écart type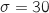 
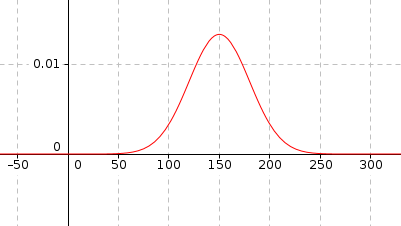
. La courbe de la densité de probabilité associée à est représentée ci-dessous.
.
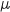La courbe de densité associée à une loi normale admet un axe de symétrie verticale d'équation
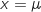. On lit sur le graphique que 
.
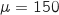2. On pêche un de ces poissons dans la zone 1. Donner la probabilité, arrondie à 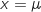. On lit sur le graphique que .
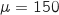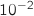, d'avoir un
poisson dont la taille est comprise entre 150 cm et 210 cm.
En utilisant la calculette on obtient directement :
.
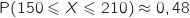3. Un poisson de cette espèce de la zone 1 est considéré comme adulte quand il mesure plus de 120 cm.
On pêche un poisson de l'espèce considérée dans la zone 1. Donner la probabilité, arrondie à .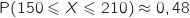
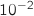, de pêcher un poisson adulte.
Il s'agit de calculer :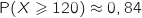 
.
.
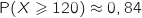4. On considère un nombre
strictement plus grand que la valeur moyenne .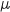
Est-il vrai que 
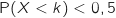? Justifier.
Un petit dessin :
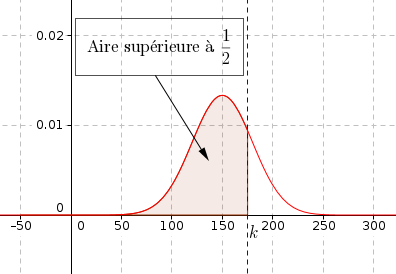
Par symétrie de la courbe de densité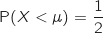 
, donc pour 
,
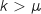on aura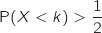 
et du coup l'affirmation est fausse.
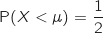, donc pour ,
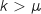on aura 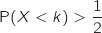et du coup l'affirmation est fausse.
B . Etude de la zone 2
1. Certains poissons de la zone 2 sont atteints d'une maladie. On prélève de façon aléatoire un échantillon de 50 poissons de cette espèce dans la zone 2 et on constate que 15 poissons sont malades. a. Calculer la fréquence
de poissons malades dans l'échantillon.
La fréquence de poissons malades dans l'échantillon est :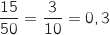 
.
b. Déterminer un intervalle de confiance, au niveau de 95 %, de la proportion .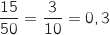
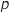de poissons malades dans toute la zone 2. On arrondira les bornes au millième.
On utilise l'intervalle de confiance vu en cours :
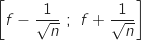
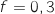et 
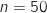ce qui donne :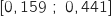 
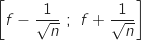
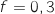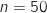2. Soit et ce qui donne :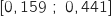
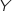la variable aléatoire qui, à chaque poisson de l'espèce considérée de la zone 2, associe sa taille en cm.
On admet que la variable aléatoire 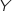suit la loi normale de moyenne 
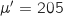et d'écart type 
.
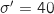En comparant avec le graphique de la zone 1 donné à la question 1 qui représente une loi normale d'écart type 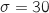, dire laquelle des trois
courbes ci-dessous représente la densité de probabilité de la variable aléatoire 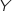. Justifier la réponse.
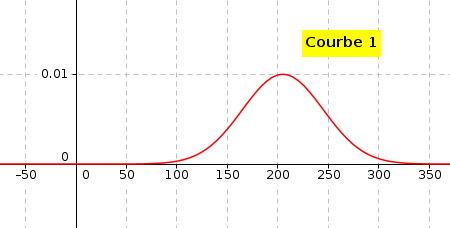
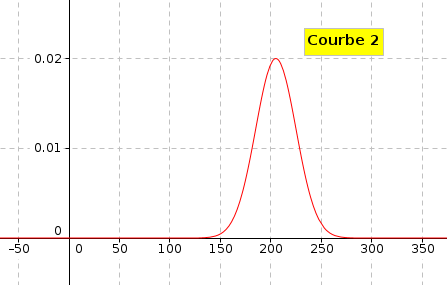
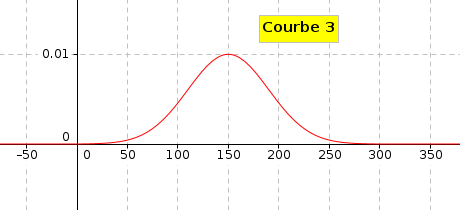
On peut déjà éliminer la courbe 3 car elle n'est pas symétrique par rapport à
la droite d'équation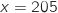 
.
En revanche les courbes 1 et 2 représentent bien des fonctions de densités
de lois normales de moyenne 
.
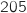On regarde maintenant l'aplatissement des courbes (les courbes étant représentées dans des repères identiques) :
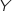qui suit une loi normale
d'écart-type 40 est la courbe 1.
.
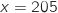En revanche les courbes 1 et 2 représentent bien des fonctions de densités
de lois normales de moyenne .
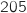On regarde maintenant l'aplatissement des courbes (les courbes étant représentées dans des repères identiques) :
- la courbe 1 est plus aplatie que la courbe de la partie A, donc la loi normale associée à un écart-type supérieur à 30.
- la courbe 2 est moins aplatie que la courbe de la partie A, donc la loi normale associée à un écart-type inférieur à 30.
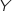qui suit une loi normale
d'écart-type 40 est la courbe 1.
