Sujet et corrigé de l'exercice de spécialité du bac ES de maths de juin 2013 en Polynésie
Cacher les corrigés
Alors qu'une entreprise A possédait le monopole de l'accès à internet des particuliers, une entreprise concurrente B est autorisée à s'implanter. Lors de l'ouverture au public en 2010 des services du fournisseur d'accès B, l'entreprise A possède 90 % du marché et l'entreprise B possède le reste du marché. Dans cet exercice, on suppose que chaque année, chaque internaute est client d'une seule entreprise A ou B. On observe à partir de 2010 que chaque année, 15 % des clients de l'entreprise A deviennent des clients de l'entreprise B, et 10% des clients de l'entreprise B deviennent des clients de l'entreprise A. Pour tout entier naturel
, on note 
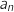la probabilité qu'un internaute de ce pays, choisi au hasard, ait son accès à internet fourni par l'entreprise
A pour l'année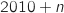 
, et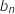 
la probabilité pour que son fournisseur d'accès en 
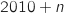soit l'entreprise B.
On note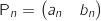 
la matrice correspondant à l'état probabiliste de l'année 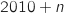et on a ainsi 
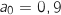et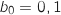 
.
Partie A
1. Représenter cette situation par un graphe probabiliste.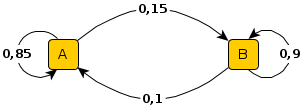
Par lecture directe sur le graphe on obtient la matrice de transistion suivante :
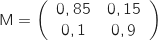
b. Montrer qu'en 2013, l'état probabiliste est environ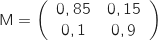 
.
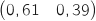L'année 2013 est de rang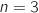 
, donc pour obtenir l'état probabiliste en 2013 on doit
multiplier 
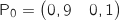par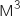 
.
En utilisant la calculette on obtient : 
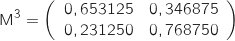puis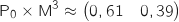 
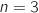, donc pour obtenir l'état probabiliste en 2013 on doit
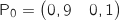multiplier par .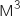
En utilisant la calculette on obtient :
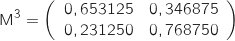puis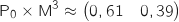
c. Déterminer l'état stable P
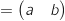de la répartition des clients des entreprises A et B. Interpréter le résultat.
L'état stable P est tel que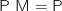 
.
On calcule déjà : 
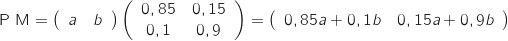et l'égalité 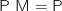donne le système :
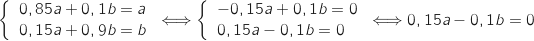On aboutit ainsi à une seule équation à deux inconnues, mais on n'oublie pas que 
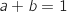ce qui donne finalement
le système :
Donc l'état stable est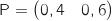 
.
La matrice de transition ne comporte pas de 0, donc l'état 
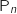du système considéré
converge vers cet état stable.
.
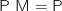On calcule déjà :
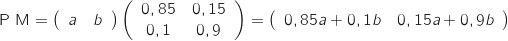et l'égalité 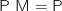donne le système :
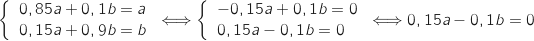On aboutit ainsi à une seule équation à deux inconnues, mais on n'oublie pas que 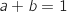ce qui donne finalement
le système :
Donc l'état stable est .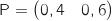
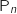La matrice de transition ne comporte pas de 0, donc l'état du système considéré
converge vers cet état stable.
Partie B
Lors d'une campagne de marketing l'entreprise B distribue un stylo ou un porte-clés ; il en coûte à l'entreprise 0,80 € par stylo et 1,20 € par porte-clés distribué. A la fin de la journée l'entreprise a distribué 550 objets et cela lui a coûté 540 €. On cherche le nombre
de stylos et le nombre 
de porte-clés distribués.
1. Ecrire un système traduisant cette situation.
A partir des données de l'énoncé on obtient facilement le système :
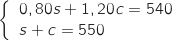
2. Montrer que le système précédent est équivalent à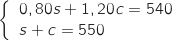
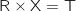où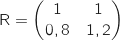 
et X et T sont des matrices que l'on précisera.
On pose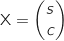 
, alors le produit 
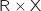donne :
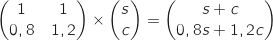En posant 
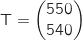, l'égalité
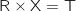équivaut au système de la question 1.
3. Résoudre le système à l'aide de la calculatrice. Interpréter le résultat.
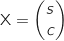, alors le produit 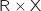donne :
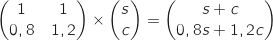En posant 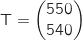, l'égalité
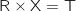équivaut au système de la question 1.
Avec la calculette on trouve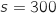 
et 
.
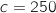L'entreprise a donc distribué 300 stylos et 250 porte-clés.
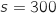et .
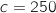L'entreprise a donc distribué 300 stylos et 250 porte-clés.
