Sujet et corrigé de l'exercice 1 du bac ES de maths de juin 2014 en Polynésie
Cacher les corrigés
Partie A
Document 1
« En France, pendant l'année scolaire 2009-2010, sur 81 135 étudiants inscrits en classe préparatoire aux grandes écoles (CPGE), on pouvait trouver 34 632 filles. »
(Source: Repères et références statistiques sur les enseignements, la formation et la recherche Edition 2010)
Selon l'INSEE, la proportion de filles parmi les jeunes entre 15 et 24 ans est de 49,2 %.
Peut-on considérer, en s'appuyant sur le document 1 que les filles inscrites sont sous-représentées en CPGE ?
Justifier la réponse.
On pourra utiliser un intervalle de fluctuation.
On teste l'hypothèse que la proportion de filles dans les CPGE est .
On veut utiliser un intervalle de fluctuation asymptotique au seuil de 95 %.
On vérifie les conditions usuelles d'utilisation :
On travaille avec étudiants, donc
, donc
, donc
L'intervalle de fluctuation considéré est :
Soit .
La proportion observée de filles dans les CPGE est de .
Comme , on rejette l'hypothèse et donc au vu de cela on peut considérer que les filles sont sous-représentées en CPGE.
Partie B
Les étudiants des CPGE se répartissent en 3 filières :
la filière scientifique (S) accueille 61,5 % des étudiants ;
la série économique et commerciale (C) accueille 24 % des étudiants ;
les autres étudiants suivent une filière littéraire (L).
Document 2
« En classes littéraires, la prépondérance des femmes semble bien implantée : avec trois inscrites sur quatre, elles y sont largement majoritaires.
Inversement, dans les préparations scientifiques, les filles sont présentes en faible proportion (30 %) alors qu'on est proche de la parité dans les classes économiques et commerciales. »
(Même source)
On considère que parmi tous les inscrits en CPGE en 2009-2010, la proportion de fille est 42,7 %.
On interroge au hasard un étudiant en CPGE.
On considère les événements suivants :
F : l'étudiant interrogé est une fille ;
S : l'étudiant interrogé est inscrit dans la filière scientifique ;
C : l'étudiant interrogé est inscrit dans la filière économique et commerciale ;
L : l'étudiant interrogé est inscrit dans la filière littéraire.
1. Donner les probabilités , , , et .
Construire un arbre pondéré traduisant cette situation. Cet arbre sera complété au fur et à mesure de l'exercice.
.
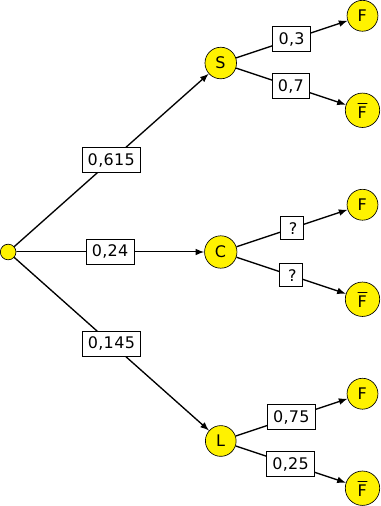
2.a. Calculer la probabilité que l'étudiant interrogé au hasard soit une fille inscrite en L.
Par la formule des probabilités composées :
b. Calculer la probabilité de l'événement .
En déduire que la probabilité de l'événement est 0,133 75.
.
Les événements S, C et L forment une partition de l'univers, du coup d'après la formule des probabilités totales :
Donc et
3. Sachant que l'étudiant interrogé suit la filière économique et commerciale, quelle est la probabilité qu'il soit une fille ?
On arrondira le résultat au millième.
Confronter ce résultat avec les informations du document 2.
Le résultat obtenu est proche de , cela correspond à l'indication du document 2 : « on est proche de la parité dans les classes économiques et commerciales ».
4. Sachant que l'étudiant interrogé est une fille, quelle est la probabilité qu'elle soit inscrite dans la filière littéraire L ?
On arrondira le résultat au millième.
.
