Sujet et corrigé de l'exercice 2 du bac ES de maths de juin 2014 en Polynésie
Cacher les corrigés
Une entreprise fabrique chaque jour des objets.
Cette production ne peut dépasser objets par jour.
On modélise le coût total de production par une fonction .
Lorsque désigne le nombre d'objets fabriqués, exprimé en centaines, , le coût total correspondant, est exprimé en centaines d'euros.
La courbe représentative de la fonction est donnée ci-dessous :
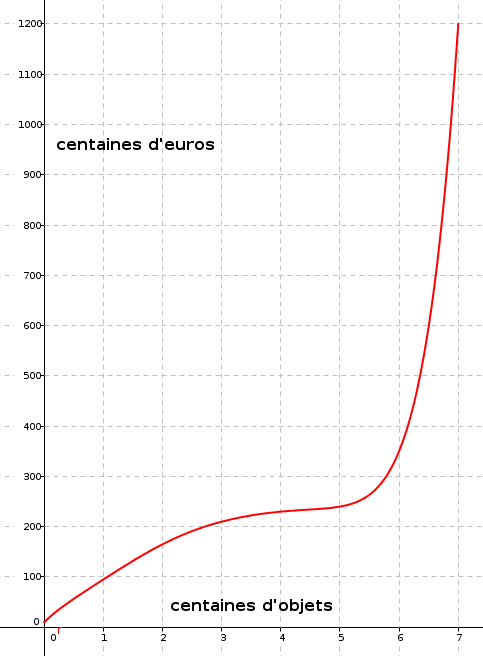
Partie A
Par lecture graphique, répondre aux questions suivantes en arrondissant au mieux.
On laissera apparents les traits de construction sur la figure.
1. Quel est le coût total de production pour 450 objets ?
2. Combien d'objets sont produits pour un coût total de 60 000 euros ?
On considère que le coût marginal est donné par la fonction dérivée de la fonction .
a. Estimer le coût marginal pour une production de 450 objets puis de 600 objets.
b. Que pensez-vous de l'affirmation :
« le coût marginal est croissant sur l'intervalle » ?
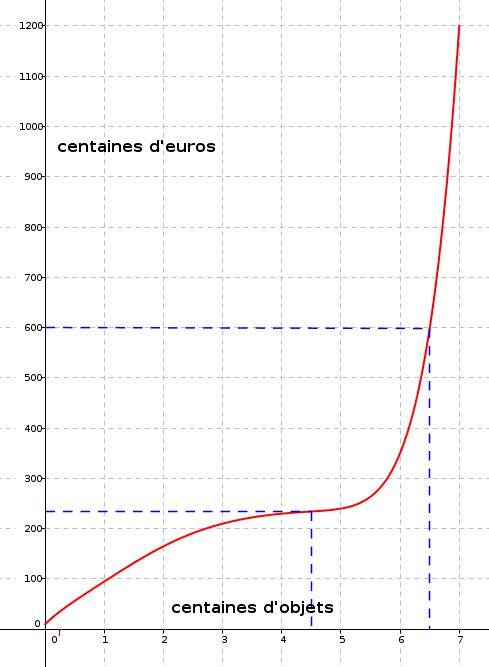
Le coût de production de 450 objets est d'environ 24 000 euros.
Pour 60 000 euros, l'entreprise fabrique environ 650 objets.
Pour une production de 450 objets le coût marginal est nul car la tangente au point d'abscisse 4,5 est parallèle à l'axe des abscisses.
Cette affirmation est fausse : la fonction est concave sur donc sur cet intervalle la dérivée et donc le coût marginal est décroissant.
Partie B
Le prix de vente de chacun de ces objets est de 75 euros.
1. On note la fonction « recette ».
Pour tout nombre réel dans l'intervalle , est le prix de vente, en centaines d'euros, de centaines d'objets.
Représenter la fonction dans le repère.
2. En utilisant les représentations graphiques, répondre aux questions qui suivent.
a. En supposant que tous les objets produits sont vendus, quelle est, pour l'entreprise, la fourchette maximale de rentabilité ?
Justifier la réponse.
b. Que penser de l'affirmation :
« il est préférable pour l'entreprise de fabriquer 500 objets plutôt que 600 objets » ?
On représente la droite d'équation .
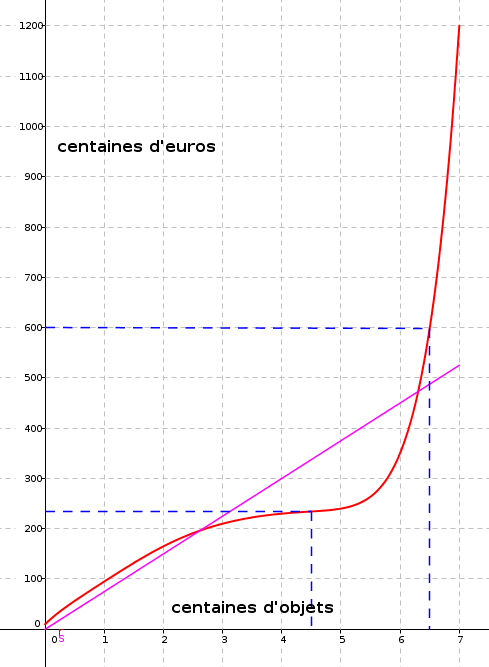
L'entreprise est rentable lorsque la recette est supérieure au coût, par lecture graphique c'est pour environ entre 270 et 630 objets fabriqués.
L'affirmation est vraie car l'écart entre le coût et la recette est plus important pour 500 objets que pour 600 objets.
Du coup l'entreprise réalise un plus grand bénéfice pour 500 objets que pour 600 objets.
