Sujet et corrigé de l'exercice 4 du bac ES de maths de juin 2014 en Polynésie
Cacher les corrigés
Les antibiotiques sont des molécules possédant la propriété de tuer des bactéries ou d'en limiter la propagation.
Le tableau ci-dessous donne la concentration dans le sang en fonction du temps d'un antibiotique injecté en une seule prise à un patient.
| Temps en heure | 0,5 | 1 | 1,5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Concentration en mg/l | 1,6 | 2 | 1,9 | 1,6 | 1,2 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,4 |
Ces données conduisent à la modélisation de la concentration en fonction du temps par la fonction définie sur l'intervalle par
Lorsque représente le temps écoulé, en heures, depuis l'injection de l'antibiotique, représente la concentration en mg/l de l'antibiotique.
Le graphique suivant représente les données du tableau et la courbe représentative de la fonction .
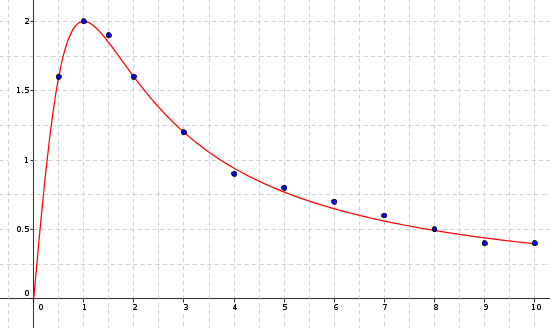
1. Par lecture graphique donner sans justification :
a. les variations de la fonction sur ;
b. la concentration maximale d'antibiotique lors des 10 premières heures ;
c. l'intervalle de temps pendant lequel la concentration de l'antibiotique dans le sang est supérieure à 1,2 mg/l.
la fonction est croissante sur et décroissante sur
la concentration maximale au cours des 10 premières heures est d'environ 2 mg/l.
la concentration de l'antibiotique dans le sang est supérieure à 1,2 mg/l entre à peu près 15 minutes et 3 heures.
2.a. La fonction est dérivable sur l'intervalle et sa dérivée est .
Montrer que :
Pour tout on a :
où
;
;
Donc :
b. En utilisant l'expression de , montrer que la concentration maximale serait, avec cette modélisation, atteinte exactement 1 heure après l'injection.
Pour tout , , donc le signe de est le même que celui de :
Les racines de l'expression du second degré en question sont et 1 ;
Du coup :
sur , ;
;
sur ,
Ainsi s'annule en 1 en changeant de signe (positif à négatif), donc la fonction admet un maximum pour .
3. On admet que définie sur par
est une primitive de sur cet intervalle.
Quelle est la concentration moyenne de l'antibiotique pendant les 10 premières heures ?
Donner la valeur exacte et la valeur arrondie au millième.
Rappel : la valeur moyenne d'une fonction sur est donnée par :
On calcule :
4. On définit la CMI (Concentration Minimale Inhibitrice) d'un antibiotique comme étant la concentration au dessus de laquelle les bactéries ne peuvent plus se multiplier.
La CMI de l'antibiotique injecté est 1,2 mg/l.
Déterminer, par le calcul, le temps d'antibiotique utile c'est-à-dire la durée pendant laquelle la concentration de l'antibiotique étudié est supérieure à sa CMI.
On résout sur :
On étudie le signe du trinôme du second degré obtenu.
Son discriminant :
Il possède deux racines :
et
L'expression trinôme est négative entre les racines et du coup :
Le temps d'antibiotique utile est alors :
h, soit 2h 40 min.
