Sujet et corrigé de l'exercice de spécialité du bac ES de maths de juin 2014 en Polynésie
Cacher les corrigés
Partie A
Le graphe ci-dessous représente, dans un aéroport donné, toutes les voies empruntées par les avions au roulage.
Ces voies, sur lesquelles circulent les avions avant ou après atterrissage, sont appelées « taxiways ».
Les arêtes du graphe représentent les voies de circulation (les « taxiways ») et les sommets du graphe sont les intersections.
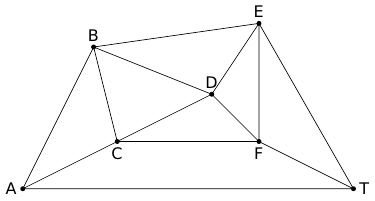
1. Déterminer le nombre de voies de circulation au total.
On compte le nombre d'arêtes du graphe.
Il y a 13 voies de circulation.
2. Afin que l'aéroport soit déneigé le plus rapidement possible, est-il possible de planifier un parcours pour que les chasse-neige passent par toutes les voies sans emprunter plusieurs fois la même route ?
Justifier la réponse et donner un tel parcours.
On détermine les degrés des sommets du graphe :
| Sommet | A | B | C | D | E | F | T |
| Degré | 3 | 4 | 4 | 4 | 4 | 4 | 3 |
On remarque que le graphe est connexe et qu'il possède exactement 2 sommets de degré impair, donc il existe une chaîne eulérienne permettant de joindre ces deux sommets pour répondre à la question posée.
Par exemple :
A, B, E, T, A, C, B, D, C, F, D, E, F, T
Partie B
Dans le graphe ci-dessous, on a indiqué le sens de circulation pour les avions dans les différentes voies ainsi que le temps de parcours pour chacune en minute( s).

1.a. Ecrire la matrice M associée à ce graphe (ranger les sommets dans l'ordre alphabétique).
b. Citer tous les chemins de longueur 3 reliant A à T.
Il y deux chemins possibles :
A, C, F, T
A, B, E, T
2. L'avion qui a atterri est en bout de piste en A et doit se rendre le plus rapidement possible au terminal situé au point T.
Déterminer l'itinéraire le plus rapide et en donner la durée.
On utilise l'algorithme de Dijsktra dont les étapes sont présentées dans le tableau ci-dessous :
| A | B | C | D | E | F | T |
| 0 | 4 ; A | 3 ; A | ||||
| / | 4,5 ; C | 5 ; C | 6 ; C | |||
| / | / | 4,5 ; B | 5 ; B | 6 ; C | ||
| / | / | / | 5 ; D | 5 ; D | ||
| / | / | / | / | 5,5 ; E | 9 ; E | |
| / | / | / | / | / | 5,5 ; F | |
| / | / | / | / | / | / |
Donc l'itinéraire le plus rapide est :
A, B, D, F, T
Sa durée est de 5,5 min, soit 5 min et 30 s.
