Corrigé de l'exercice 1 du bac ES de maths d'avril 2012 à Pondichéry
Cacher les corrigés
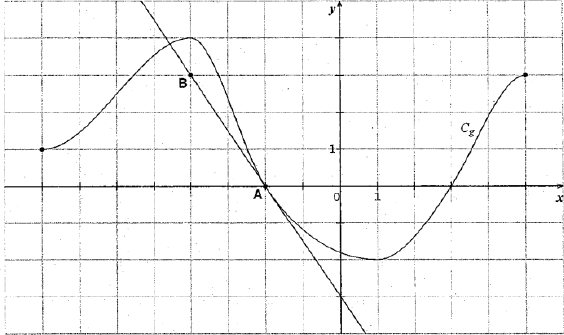
Cet exercice est un questionnaire à choix multiples. Il est constitué de quatre questions indépendantes. Pour chacune des questions posées, une seule des trois réponses proposées est exacte. Recopier le numéro de chaque question et indiquer la réponse choisie. Aucune justification n'est demandée. Une réponse exacte rapporte 1 point, une réponse fausse ou l'absence de réponse n'apporte ni n'enlève aucun point. 1. La courbe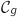 tracée ci-dessous est la représentation graphique d'une fonction
tracée ci-dessous est la représentation graphique d'une fonction  définie et dérivable sur l'intervalle
définie et dérivable sur l'intervalle 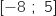 .
La droite (AB) tracée sur le graphique est la tangente à la courbe
.
La droite (AB) tracée sur le graphique est la tangente à la courbe 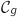 au point A d'abscisse
au point A d'abscisse 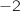 .
On note
.
On note 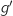 la fonction dérivée da la fonction
la fonction dérivée da la fonction  sur l'intervalle
sur l'intervalle 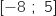 .
.
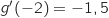 b.
b. 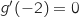 c.
c. 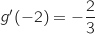 .
.
Le nombre dérivé de  au point A d'abscisse
au point A d'abscisse 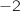 est le coefficient directeur de la droite (AB).
Par lecture graphique on lit
est le coefficient directeur de la droite (AB).
Par lecture graphique on lit 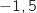 , donc
, donc 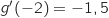 .
La bonne réponse est la réponse a.
.
La bonne réponse est la réponse a.
 au point A d'abscisse
au point A d'abscisse 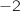 est le coefficient directeur de la droite (AB).
Par lecture graphique on lit
est le coefficient directeur de la droite (AB).
Par lecture graphique on lit 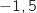 , donc
, donc 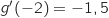 .
La bonne réponse est la réponse a.
.
La bonne réponse est la réponse a.
2. On note
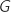 une primitive sur l'intervalle
une primitive sur l'intervalle 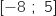 de la fonction
de la fonction  introduite à la question 1.
a. la fonction
introduite à la question 1.
a. la fonction 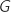 admet un minimum en
admet un minimum en 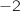 b. la fonction
b. la fonction 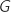 est décroissante sur l'intervalle
est décroissante sur l'intervalle 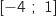 c. la fonction
c. la fonction 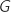 est croissante sur l'intervalle
est croissante sur l'intervalle 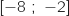 .
.
On a pour tout 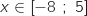 ,
, 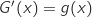 , donc le signe de
, donc le signe de  donne les variations de
donne les variations de 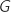 .
En particulier, pour tout
.
En particulier, pour tout 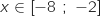 ,
, 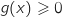 et ne s'annule que pour
et ne s'annule que pour 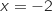 , donc
, donc 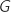 est croissante sur cet intervalle.
La bonne réponse est la réponse c.
est croissante sur cet intervalle.
La bonne réponse est la réponse c.
3. Soit 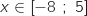 ,
, 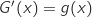 , donc le signe de
, donc le signe de  donne les variations de
donne les variations de 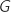 .
En particulier, pour tout
.
En particulier, pour tout 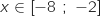 ,
, 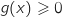 et ne s'annule que pour
et ne s'annule que pour 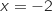 , donc
, donc 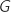 est croissante sur cet intervalle.
La bonne réponse est la réponse c.
est croissante sur cet intervalle.
La bonne réponse est la réponse c.
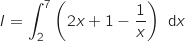 a.
a. 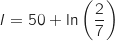 b.
b. 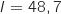 c.
c. 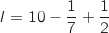 .
.
Une primitive sur 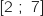 de la fonction
de la fonction 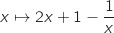 est
est 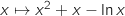 , donc :
, donc :
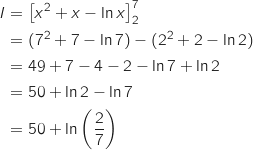 La bonne réponse est la réponse a.
La bonne réponse est la réponse a.
4. Soit 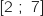 de la fonction
de la fonction 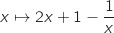 est
est 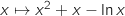 , donc :
, donc :
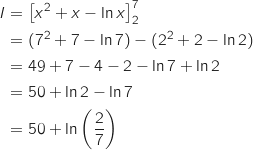 La bonne réponse est la réponse a.
La bonne réponse est la réponse a.
 la fonction définie sur l'ensemble
la fonction définie sur l'ensemble  des nombres réels par :
des nombres réels par :
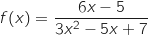
 la primitive de
la primitive de  sur
sur  telle que
telle que 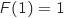 .
a. Pour tout
.
a. Pour tout  de
de  ,
, 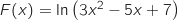 b. Pour tout
b. Pour tout  de
de  ,
, 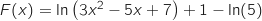 c. Pour tout
c. Pour tout  de
de  ,
, 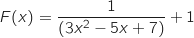
On remarque que 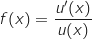 avec
avec 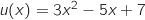 .
Donc les primitives de
.
Donc les primitives de  sur
sur  sont de la forme :
sont de la forme : 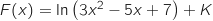 .
La condition
.
La condition 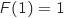 donne :
donne :
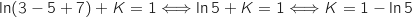 .
Donc
.
Donc 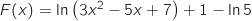 .
La bonne réponse est la réponse b.
.
La bonne réponse est la réponse b.
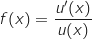 avec
avec 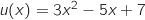 .
Donc les primitives de
.
Donc les primitives de  sur
sur  sont de la forme :
sont de la forme : 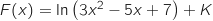 .
La condition
.
La condition 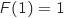 donne :
donne :
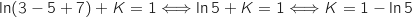 .
Donc
.
Donc 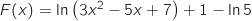 .
La bonne réponse est la réponse b.
.
La bonne réponse est la réponse b.
