Corrigé de l'exercice 3 de maths du bac ES d'avril 2012 à Pondichéry
Cacher les corrigés
Un fournisseur d'accès internet effectue une enquête de satisfaction sur un panel de 2000 clients, dont l'abonnement a plus de 12 mois d'ancienneté. Parmi eux :- 900 n'ont jamais subi de coupure prolongée de connexion.
- 500 clients ont connu leur dernière coupure prolongée de connexion dans les 12 derniers mois.
- les autres clients ont connu leur dernière coupure prolongée de connexion il y a plus d'un an.
- 95% des clients n'ayant jamais subi de coupure prolongée se déclarent satisfaits du service fourni.
- 50% des clients ayant subi une coupure prolongée de connexion dans les douze derniers mois se déclarent satisfaits du service fourni.
- 70% des clients ayant subi une coupure prolongée de connexion il y a plus d'un an se déclarent satisfaits du service fourni.
On choisit au hasard un client parmi ceux qui ont été interrogés. On considère les événements suivants : J : « le client n'a jamais subi de coupure prolongée de connexion » R : « la dernière coupure prolongée de connexion du client est survenue au cours des douze derniers mois » (elle est « récente ») A : « la dernière coupure prolongée de connexion du client date d'il y a plus d'un an » (elle est « ancienne ») S : « le client se déclare satisfait »
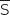désigne l'événement contraire de S.
1.a. Calculer les probabilités des événements J, R et A.
Il y a 900 clients sur 2000 qui n'ont jamais subi de coupure prolongée donc :
.
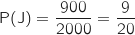Il y a 500 clients sur 2000 qui ont subi une coupure prolongée récente donc :
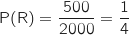Il y a 
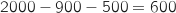clients qui ont subi une coupure prolongée ancienne donc :
.
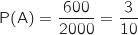
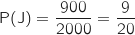Il y a 500 clients sur 2000 qui ont subi une coupure prolongée récente donc :
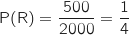Il y a 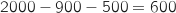clients qui ont subi une coupure prolongée ancienne donc :
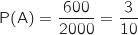
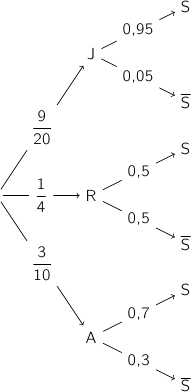
b. Construire un arbre pondéré décrivant la situation, en indiquant sur chaque branche la probabilité correspondante.
On calcule la probabilité de l'événément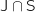 
en utilisant la formule des probabilités composées (principe multiplicatif sur l'arbre).
.
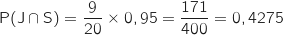3. Démontrer que la probabilité que le client choisi se déclare satisfait est égale à 0,7625.
en utilisant la formule des probabilités composées (principe multiplicatif sur l'arbre).
.
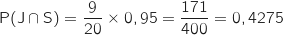Les événements J, R et A constituent ensemble un système complet d'événements, donc d'après la formule des probabilités totales on a :
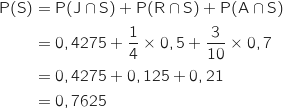
4. Le client choisi se déclare satisfait du service fourni.
Quelle est la probabilité qu'il ait subi une coupure prolongée de connexion au cours des douze derniers mois (on donnera le résultat sous forme décimale arrondie au centième) ?
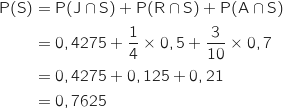
On cherche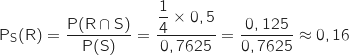 
.
5. On choisit au hasard trois clients parmi ceux du panel interrogé durant l'enquête. On admet que ce panel est suffisamment important pour assimiler ces choix à des tirages successifs
indépendants avec remise.
Déterminer la probabilité qu'exactement un des clients choisis se déclare non satisfait du service fourni (on donnera le résultat sous forme décimale arrondie au centième).
.
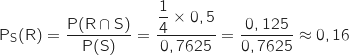On répète de façon indépendante une expérience de Bernoulli, donc la variable aléatoire 
qui compte le nombre de personnes satisfaites suit une loi binomiale de paramètres 3 et 0,7625.
L'événement « exactement un client est non satisfait » équivaut à « exactement deux clients sont satisfaits » soit « 
».
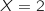On a, en utilisant la formule du cours pour une loi binomiale :
.
qui compte le nombre de personnes satisfaites suit une loi binomiale de paramètres 3 et 0,7625.
L'événement « exactement un client est non satisfait » équivaut à « exactement deux clients sont satisfaits » soit « ».
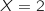On a, en utilisant la formule du cours pour une loi binomiale :
.
