Corrigé de l'exercice 4 du bac ES de maths d'avril 2012 à Pondichéry
Cacher les corrigés
Partie A
On considère la fonction définie sur
définie sur  par :
par :
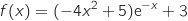
 la courbe représentative de la fonction
la courbe représentative de la fonction  dans un repère orthogonal.
1. On note
dans un repère orthogonal.
1. On note 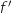 la fonction dérivée de la fonction
la fonction dérivée de la fonction  sur l'intervalle
sur l'intervalle  .
a. Démontrer que pour tout réel
.
a. Démontrer que pour tout réel  de
de  , on a :
, on a :
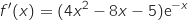
On remarque que 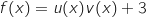 , avec :
, avec :
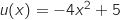 et
et 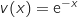 , d'où
, d'où 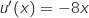 et
et 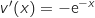 .
En utilisant la formule de la dérivée d'un produit on a :
.
En utilisant la formule de la dérivée d'un produit on a :
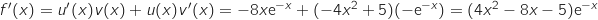
b. Etudier le signe de la fonction 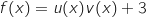 , avec :
, avec :
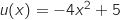 et
et 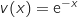 , d'où
, d'où 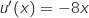 et
et 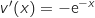 .
En utilisant la formule de la dérivée d'un produit on a :
.
En utilisant la formule de la dérivée d'un produit on a :
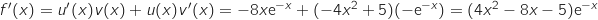
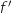 sur l'intervalle
sur l'intervalle  .
.
Pour tout 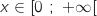 ,
, 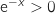 , donc le signe de
, donc le signe de  est le même que celui de
est le même que celui de 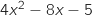 .
Il s'agit d'un trinôme du second degré dont le discriminant est
.
Il s'agit d'un trinôme du second degré dont le discriminant est 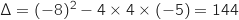 .
Ce trinôme admet deux racines qui sont :
.
Ce trinôme admet deux racines qui sont :
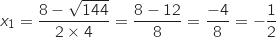
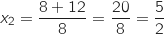 .
On en déduit le signe de ce trinôme sur
.
On en déduit le signe de ce trinôme sur  :
:

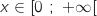 ,
, 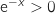 , donc le signe de
, donc le signe de  est le même que celui de
est le même que celui de 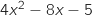 .
Il s'agit d'un trinôme du second degré dont le discriminant est
.
Il s'agit d'un trinôme du second degré dont le discriminant est 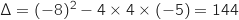 .
Ce trinôme admet deux racines qui sont :
.
Ce trinôme admet deux racines qui sont :
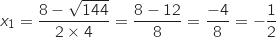
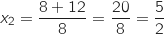 .
On en déduit le signe de ce trinôme sur
.
On en déduit le signe de ce trinôme sur  :
:

2.a. Démontrer que pour tout
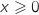 , on a
, on a 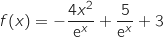 .
.
On écrit 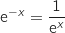 ce qui donne :
ce qui donne :
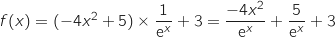 .
.
b. En déduire la limite de la fonction 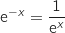 ce qui donne :
ce qui donne :
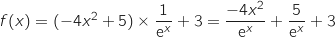 .
.
 en
en  .
(On pourra utiliser le résultat suivant :
.
(On pourra utiliser le résultat suivant : 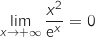 ).
).
On sait que 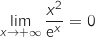 , donc par produit :
, donc par produit : 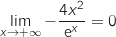 .
.
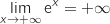 et par inverse
et par inverse 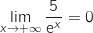 .
Finalement par addition,
.
Finalement par addition, 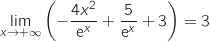 .
.
c. Interpréter graphiquement cette limite.
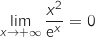 , donc par produit :
, donc par produit : 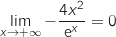 .
.
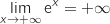 et par inverse
et par inverse 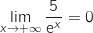 .
Finalement par addition,
.
Finalement par addition, 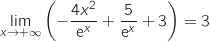 .
.
On en déduit que la courbe 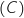 admet une asymptote « horizontale » d'équation
admet une asymptote « horizontale » d'équation 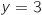 en
en  .
.
3. A l'aide des questions 1. et 2., dresser le tableau de variation de la fonction 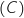 admet une asymptote « horizontale » d'équation
admet une asymptote « horizontale » d'équation 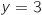 en
en  .
.
 .
.
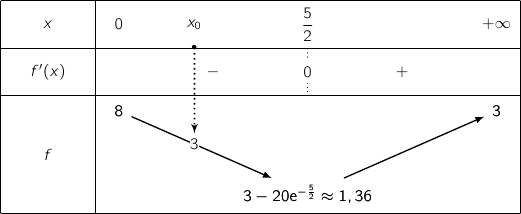
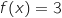 admet une unique solution
admet une unique solution 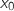 dans l'intervalle
dans l'intervalle  .
Donner une valeur approchée de
.
Donner une valeur approchée de 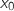 à
à 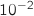 près.
près.
Par lecture sur le tableau de variation, on remarque que pour 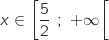 ,
, 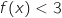 .
En revanche sur
.
En revanche sur 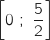 , la fonction
, la fonction  est continue et strictement décroissante, avec
est continue et strictement décroissante, avec 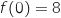 et
et 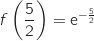 .
Comme
.
Comme 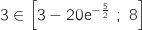 , on peut dire d'après le théorème des valeurs intermédiaires que l'équation
, on peut dire d'après le théorème des valeurs intermédiaires que l'équation 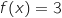 admet une unique solution dans
admet une unique solution dans 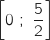 .
Par balayage, en utilisant la calculette on trouve
.
Par balayage, en utilisant la calculette on trouve 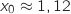 .
.
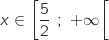 ,
, 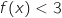 .
En revanche sur
.
En revanche sur 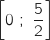 , la fonction
, la fonction  est continue et strictement décroissante, avec
est continue et strictement décroissante, avec 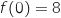 et
et 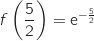 .
Comme
.
Comme 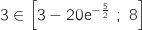 , on peut dire d'après le théorème des valeurs intermédiaires que l'équation
, on peut dire d'après le théorème des valeurs intermédiaires que l'équation 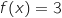 admet une unique solution dans
admet une unique solution dans 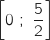 .
Par balayage, en utilisant la calculette on trouve
.
Par balayage, en utilisant la calculette on trouve 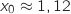 .
.
Partie B
Une entreprise produit de la peinture qu'elle vend ensuite. Toute la production est vendue. Le coût moyen unitaire de cette production peut être modélisé par la fonction de la partie A :
pour
de la partie A :
pour  hectolitres de peinture fabriqués (avec
hectolitres de peinture fabriqués (avec 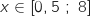 ), le nombre
), le nombre 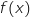 désigne le coût moyen
unitaire de production par hectolitre de peinture, exprimé en centaines d'euros (on rappelle qu'un
hectolitre est égal à 100 litres).
Dans la suite de l'exercice, on utilise ce modèle. On pourra utiliser les résultats de la partie A. Chaque
réponse sera justifiée.
1. Déterminer le coût moyen unitaire de production en euros, arrondi à l'euro près, pour une
production de 500 litres de peinture.
désigne le coût moyen
unitaire de production par hectolitre de peinture, exprimé en centaines d'euros (on rappelle qu'un
hectolitre est égal à 100 litres).
Dans la suite de l'exercice, on utilise ce modèle. On pourra utiliser les résultats de la partie A. Chaque
réponse sera justifiée.
1. Déterminer le coût moyen unitaire de production en euros, arrondi à l'euro près, pour une
production de 500 litres de peinture.
500 litres correspond à 5 hectolitre, donc il faut calculer : 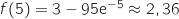 .
Donc le coût moyen unitaire de 500 litres de peinture est d'environ 236 euros.
.
Donc le coût moyen unitaire de 500 litres de peinture est d'environ 236 euros.
2.a. Combien de litres de peinture l'entreprise doit-elle produire pour minimiser le coût moyen
unitaire de production ? Quel est alors ce coût, arrondi à l'euro près ?
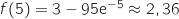 .
Donc le coût moyen unitaire de 500 litres de peinture est d'environ 236 euros.
.
Donc le coût moyen unitaire de 500 litres de peinture est d'environ 236 euros.
L'étude de la fonction  a mis en évidence un minimum atteint pour
a mis en évidence un minimum atteint pour 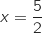 et qui vaut environ 1,36.
On en déduit que le coût moyen unitaire de production est minimum pour une production de 250 litres de peinture et qu'il vaut environ 136 euros.
et qui vaut environ 1,36.
On en déduit que le coût moyen unitaire de production est minimum pour une production de 250 litres de peinture et qu'il vaut environ 136 euros.
b. Le prix de vente d'un hectolitre de peinture est fixé à 100 euros. A l'aide de la question précédente, déterminer si l'entreprise peut réaliser des bénéfices.
 a mis en évidence un minimum atteint pour
a mis en évidence un minimum atteint pour 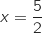 et qui vaut environ 1,36.
On en déduit que le coût moyen unitaire de production est minimum pour une production de 250 litres de peinture et qu'il vaut environ 136 euros.
et qui vaut environ 1,36.
On en déduit que le coût moyen unitaire de production est minimum pour une production de 250 litres de peinture et qu'il vaut environ 136 euros.
Le coût minimum d'un hectolitre est de 136 euros, donc si le prix de vente est seulement de 100 euros, l'entreprise ne peut pas réaliser de bénéfice.
Pour cette question, toute trace de recherche même incomplète, ou d'initiative même non
fructueuse, sera prise en compte dans l'évaluation.
3. Le prix de vente d'un hectolitre de peinture est fixé à 300 euros.
On appelle seuil de rentabilité la quantité à partir de laquelle la production est rentable, c'est-à-dire qu'elle permet à l'entreprise de réaliser un bénéfice.
Quel est le seuil de rentabilité pour cette entreprise ?
On cherche à savoir pour quelle production le coût moyen d'un hectolitre est inférieur à 300 euros, pour cela on résout l'inéquation 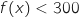 , pour
, pour 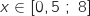 .
On a vu dans la partie A, que l'équation
.
On a vu dans la partie A, que l'équation 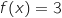 , n'avait qu'une solution dans
, n'avait qu'une solution dans  et en utilisant le tableau de variations de
et en utilisant le tableau de variations de  on peut dire que :
on peut dire que :
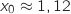 hectolitres (soit 112 litres).
hectolitres (soit 112 litres).
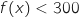 , pour
, pour 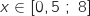 .
On a vu dans la partie A, que l'équation
.
On a vu dans la partie A, que l'équation 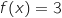 , n'avait qu'une solution dans
, n'avait qu'une solution dans  et en utilisant le tableau de variations de
et en utilisant le tableau de variations de  on peut dire que :
on peut dire que :
- pour
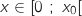 ,
, 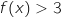 , donc pour une production de 0 à
, donc pour une production de 0 à 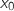 hectolitres, l'entreprise perd de l'argent,
hectolitres, l'entreprise perd de l'argent,
- pour
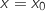 ,
, 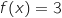 , donc pour une production de
, donc pour une production de 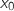 hectolitres, l'entreprise ne gagne ni ne perd de l'argent,
hectolitres, l'entreprise ne gagne ni ne perd de l'argent,
- pour
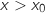 ,
, 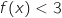 , donc pour une production de plus de
, donc pour une production de plus de 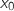 hectolitres, l'entreprise gagne de l'argent.
hectolitres, l'entreprise gagne de l'argent.
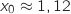 hectolitres (soit 112 litres).
hectolitres (soit 112 litres).
