Corrigé de l'exercice 2 du bac ES de maths d'avril 2013 à Pondichéry
Cacher les corrigés
Une enquête a été réalisée auprès des élèves d'un lycée afin de connaître leur point de vue sur la durée de la pause du midi ainsi que sur les rythmes scolaires. L'enquête révèle que 55% des élèves sont favorables à une pause plus longue le midi et parmi ceux qui souhaitent une pause plus longue,95% sont pour une répartition des cours plus étalée sur l'année scolaire. Parmi ceux qui ne veulent pas de pause plus longue le midi, seulement 10% sont pour une répartition des cours plus étalée sur l'année scolaire.
On choisit un élève au hasard dans le lycée. On considère les événements suivants : L : « l'élève choisi est favorable à une pause plus longue le midi » ; C : « l'élève choisi souhaite une répartition des cours plus étalée sur l'année scolaire ». 1. Construire un arbre pondéré décrivant la situation.
En lisant l'énoncé on obtient facilement l'arbre suivant :
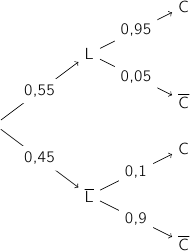
2. Calculer
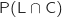la probabilité de l'évènement 
.
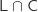Par multiplication sur les branches de l'arbre (formule des probabilités composées) on obtient :
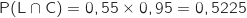
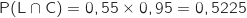
3. Montrer que
.
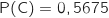Les événements L et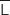 
forment une partition de l'univers, avec la formule des probabilités totales on a :
.
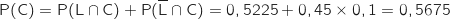(Pour le calcul de 
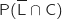on utilise la multiplication sur les branches de l'arbre comme dans la question 2.).
4. Calculer 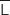forment une partition de l'univers, avec la formule des probabilités totales on a :
.
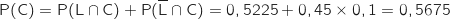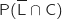(Pour le calcul de on utilise la multiplication sur les branches de l'arbre comme dans la question 2.).
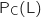, la probabilité de l'événement L sachant l'évènement C réalisé. En donner une valeur arrondie à 
.
.
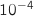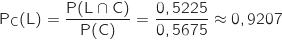la variable aléatoire qui donne le nombre d'élèves favorables à une répartition des cours plus étalée sur l'année scolaire.
Le nombre d'élèves étant suffisamment grand, on considère que suit une loi binomiale.
a) Préciser les paramètres de cette loi binomiale.
Il y a 4 répétitions indépendantes d'une expérience de Bernoulli dont le succès (événement C) a une probabilité de 0,5675.
La variable aléatoire qui compte le nombre de succès suit une loi binomiale de paramètres 
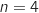et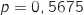 
que l'on note aussi 
.
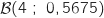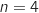b) Calculer la probabilité qu'aucun des quatre élèves interrogés ne soit favorable à une répartition des cours plus étalée sur l'année scolaire. En donner une valeur arrondie à qui compte le nombre de succès suit une loi binomiale de paramètres et 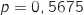que l'on note aussi .
.
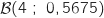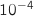Il s'agit de calculer :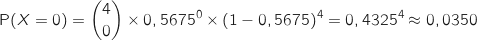 
.
c) Calculer la probabilité qu'exactement deux élèves soient favorables à une répartition des cours plus étalée sur l'année scolaire.
.
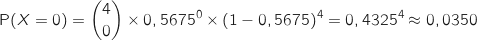Cette fois on calcule :
.
.
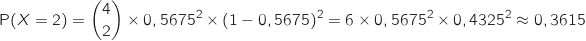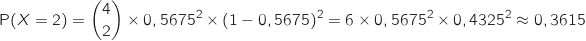