Corrigé de l'exercice 3 du bac ES de maths d'avril 2013 à Pondichéry
Cacher les corrigés
Le 1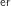
janvier 2000, un client a placé 3000 € à intérêts composés au taux annuel de 2,5%.
On note 
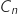le capital du client au 1 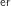janvier de l'année 
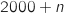, où 
est un entier naturel.
1. Calculer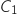 
et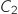 
. Arrondir les résultats au centime d'euro.
Le coefficient multiplicateur associé à l'augmentation de capital est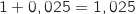 
et on a :
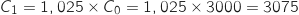
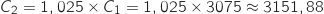
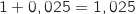et on a :
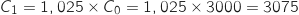
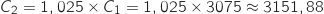
2. Exprimer
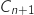en fonction de 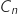. En déduire que, pour tout nombre entier naturel , on a la relation :
.
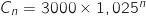D'une année à l'autre le capital subit une hausse de 2,5%,
ce qui revient à le multiplier par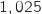 
et ce qui donne la relation 
.
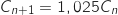Du coup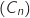 
est une suite géométrique de premier terme 
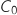et de raison 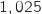dont la formule explicite est 
.
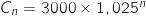3. On donne l'algorithme suivant :
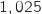et ce qui donne la relation .
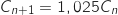Du coup 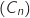est une suite géométrique de premier terme 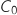et de raison 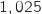dont la formule explicite est .
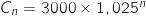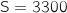saisie, recopier et compléter autant que nécessaire le tableau suivant. Les résultats seront arrondis à l'unité.
En faisant « tourner » l'algorithme à la main on obtient :
b. En déduire l'affichage obtenu quand la valeur de S saisie est 3300.
La boucle s'arrête lorsque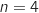 
, donc l'affichage obtenu est 2004.
c. Dans le contexte de cet exercice, expliquer comment interpréter le nombre obtenu en sortie de cet algorithme quand on saisit un nombre S supérieur à 3000.
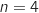, donc l'affichage obtenu est 2004.
L'algorithme détermine la première année à partir de laquelle au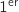 
janvier le capital atteint ou dépasse la somme S saisie en entrée.
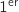janvier le capital atteint ou dépasse la somme S saisie en entrée.
4. Au 1
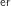janvier 2013, le client avait besoin d'une somme de 5000 €. Montrer que le capital de son placement n'est pas suffisant à cette date.
Le capital au 1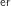 janvier de l'année 2013 est obtenu pour 
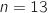, en utilisant la formule de la question 2 cela donne :
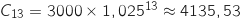Cette somme est inférieure à 5000 €, le capital n'est pas suffisant.
5. Déterminer, en détaillant la méthode, à partir du 1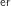 janvier de l'année 2013 est obtenu pour 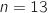, en utilisant la formule de la question 2 cela donne :
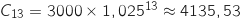Cette somme est inférieure à 5000 €, le capital n'est pas suffisant.
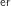janvier de quelle année le client pourrait avoir son capital initial multiplié par 10.
On cherche tel que 
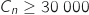, c'est à dire : 
.
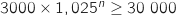On peut déjà simplifier l'inégalité par 3000 :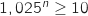 
.
Pour trouver on applique la fonction logarithme à l'inégalité de nombres positifs (sans changer le sens de l'inégalité car la fonction logarithme est strictement croissante sur
) :
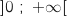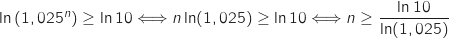(A la dernière étape on divise l'inégalité par 
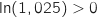, donc pas de changement de sens).
On a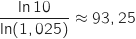 
et du coup le capital dépasse 10 fois le capital initial pour la première fois l'année de rang 94, soit le 1 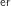janvier 2094.
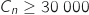tel que , c'est à dire : .
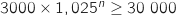On peut déjà simplifier l'inégalité par 3000 : .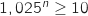
Pour trouver on applique la fonction logarithme à l'inégalité de nombres positifs (sans changer le sens de l'inégalité car la fonction logarithme est strictement croissante sur
) :
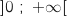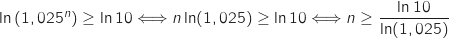(A la dernière étape on divise l'inégalité par 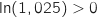, donc pas de changement de sens).
On a 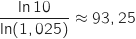et du coup le capital dépasse 10 fois le capital initial pour la première fois l'année de rang 94, soit le 1 janvier 2094.
