Corrigé de l'exercice de spécialité du bac ES de maths d'avril 2013 à Pondichéry
Cacher les corrigés
On considère le graphe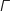
ci-dessous :
Partie A
1. Ce graphe admet-il une chaîne eulérienne ? Justifier la réponse. Si oui donner une telle chaîne.
Tableau avec les degrés des sommets du graphe :
On remarque que le graphe est connexe et que tous ses sommets sont de degré pair sauf les sommets D et G.
Donc il existe une chaîne eulérienne entre les sommets D et G.
Par exemple :
D,B,C,D,F,C,A,B,E,G,D,E,F,G
2. Ce graphe admet-il un cycle eulérien ? Justifier la réponse. Si oui donner un tel cycle.
Comme on l'a vu dans la question précédente tous les sommets du graphe ne sont pas pairs donc il n'y a pas de cycle eulérien.
3. Donner la matrice M associée au graphe . Les sommets seront pris dans l'ordre alphabétique : A, B, C, D, E, F, G.
La matrice d'adjacence du graphe est la suivante :
Partie B
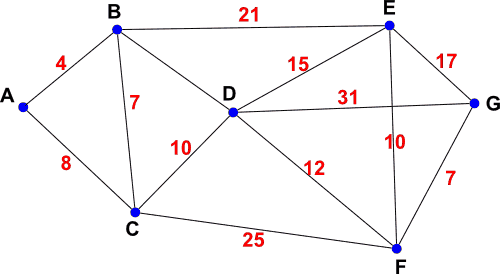
Une région est munie d'un réseau de trains, représenté par le graphe ci-dessous.
Les stations sont symbolisées par les sommets A, B, C, D, E, F et G. Chaque arête représente une ligne
reliant deux gares. Les temps de parcours (correspondance comprise) en minutes entre chaque sommet ont été rajoutés sur le graphe.
On utilise l'algorithme de Dijkstra.
Les différentes étapes sont regroupées dans le tableau suivant, lorsqu'un sommet est fixé les informations le concernant sont mises en gras.
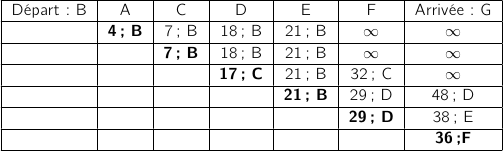
Le plus court chemin en minute reliant la gare B à la gare G est : B,C,D,F,G.
Il dure 36 minutes.
