Sujet et corrigé de l'exercice 1 du bac ES de maths de avril 2014 à Pondichéry
Cacher les corrigés
Pour chacune des propositions, déterminer si la proposition est vraie ou fausse et justifier la réponse. 1. La courbe représentative d'une fonction définie et dérivable sur est représentée ci-dessous :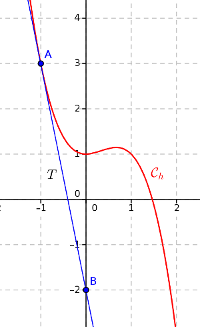
Le coefficient directeur de :
Donc
La proposition est fausse.
2. On désigne par une fonction définie et deux fois dérivable sur . La courbe représentative de la fonction , dérivée seconde de la fonction , est donnée ci-dessous :
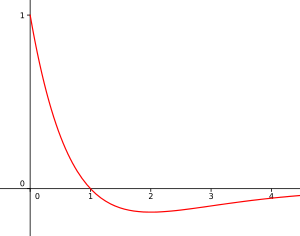
Pour tout , , donc est concave
sur l'intervalle considéré.
La proposition est fausse.
3. Proposition : on a l'égalité
La proposition est vraie.
4. La courbe représentative d'une fonction définie et continue sur l'intervalle est donnée ci-dessous :
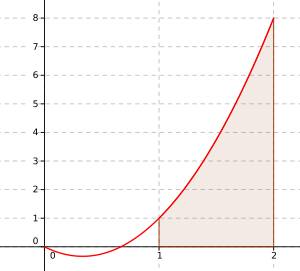
Sur est positive et continue.
Aire du domaine grisé :
La proposition est vraie.
