Sujet et corrigé de l'exercice 3 du bac ES de maths d'avril 2014 à Pondichéry
Cacher les corrigés
Partie A
Une société s'est intéressée à la probabilité qu'un de ses salariés, choisi au hasard, soit absent durant une semaine donnée de l'hiver 2014. On a évalué à la probabilité qu'un salarié ait la grippe une semaine donnée. Si le salarié a la grippe, il est alors absent. Si le salarié n'est pas grippé cette semaine là, la probabilité qu'il soit soit absent est estimée à . On choisit un salarié de la société au hasard et on considère les événements suivants :- G : le salarié a la grippe une semaine donnée ;
- A : le salarié est absent une semaine donnée.
1. Reproduire et compléter l'arbre en indiquant les probabilités de chacune des branches.
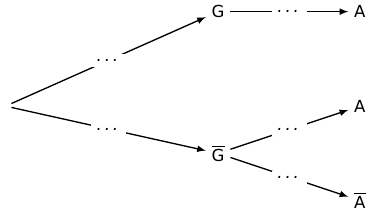
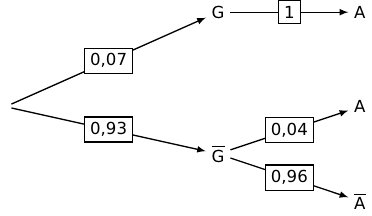
2. Montrer que la probabilité de l'événement A est égale à .
et forment une partition de l'univers.
Formule des probabilités totales :
Donc :
3. Pour une semaine donnée, calculer la probabilité qu'un salarié ait la grippe sachant qu'il est absent. Donner un résultat arrondi au millième.
.
Partie B
On admet que le nombre de journées d'absence annuel d'un salarié peut être modélisé par une variable aléatoire qui suit la loi normale de moyenne et d'écart type . 1. Justifier, en utilisant un résultat du cours, que .
Quand suit la loi normale de moyenne et d'écart type ,
on sait que .
Ici et ,
ce qui justifie la valeur de la probabilité indiquée.
2. Calculer la probabilité arrondie au millième, qu'un salarié comptabilise au moins 10 journées d'absences dans l'année.
Avec la calculette on détermine : .
Partie C
Une mutuelle déclare que 22 % de ses adhérents ont dépassé 20 journées d'absence au travail en 2013. Afin d'observer la validité de cette affirmation, un organisme enquête sur un échantillon de 200 personnes, choisies au hasard et de façon indépendante, parmi les adhérents de la mutuelle. Parmi celle-ci, 28 ont comptabilisé plus de 20 journées d'absence en 2013. Le résultat de l'enquête remet-il en question l'affirmation de la mutuelle ? Justifier la réponse. On pourra s'aider du calcul d'un intervalle de fluctuation.
Taille de l'échantillon :
Proportion d'adhérents à plus de 20 jours d'absence annoncée : .
On a : ; donc ; donc .
Intervalle de fluctuation asymptotique au seuil de 95 % :
soit
.
La proportion d'adhérents à plus de 20 jours d'absence observée est :
.
, donc le résultat de l'enquête remet en question la déclaration de la mutuelle.
