Sujet et corrigé de l'exercice 4 du bac ES de maths d'avril 2014 à Pondichéry
Cacher les corrigés
Un artisan glacier commercialise des << sorbets bio >>. Il peut en produire entre 0 et 300 litres par semaine. Cette production est vendue dans sa totalité. Le coût total de fabrication est modélisé par la fonction définie pour tout nombre réel de l'intervalle par . Lorsque représente le nombre de centaines de litres de sorbet, est le coût total de fabrication en centaines d'euros. La recette, en centaines d'euros, est donnée par une fonction définie sur le même intervalle .
Partie A
La courbe représentative de la fonction et la droite représentative de la fonction linéaire sont données ci-dessous :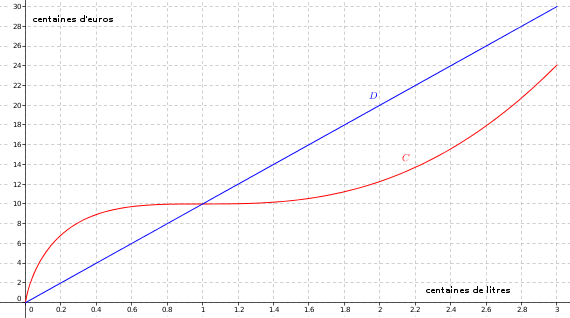
10 centaines d'euros soit 1000 euros.
b. Donner l'expression de en fonction de .
Pour dégager un bénéfice l'artisan doit produire plus de 100 litres de sorbet.
2. On admet que .
a. En déduire la valeur de .
Valeur moyenne de sur : .
Pour une production entre 100 et 300 litres, le coût moyen de la production est d'environ 1390 euros.
Partie B
On note le bénéfice réalisé par l'artisan pour la vente de centaines de litres de sorbet produit. D'après les données précédentes, pour tout de l'intervalle , on a :où est exprimé en centaines d'euros. 1. On note la fonction dérivée de la fonction . Montrer que, pour tout nombre de l'intervalle , on a : .
La dérivée de est
Pour la dérivée de , formule de la dérivée du produit :
soit
Donc
2. On donne le tableau de variation de la fonction sur l'intervalle .
est continue et strictement décroissante sur avec :
Bien sûr , donc d'après le théorème de la valeur intermédiaire a une unique solution dans .
Avec la calculette on trouve .
b. En déduire le signe de sur l'intervalle puis dresser le tableau de variation de la fonction sur ce même intervalle.
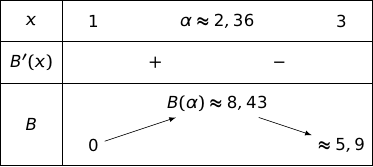
D'après l'étude précédente le bénéfice maximal que l'artisan peut atteindre est environ 843 euros.
Donc ce n'est pas envisageable.
