Sujet et corrigé de l'exercice 3 du bac ES de maths d'avril 2015 à Pondichéry
Cacher les corrigés
On s'intéresse à la fonction définie sur par
PARTIE A
1. Calculer et en donner une valeur approchée à près.
2. Justifier que où est la fonction dérivée de .
La fonction se présente sous la forme avec :
;
;
Donc
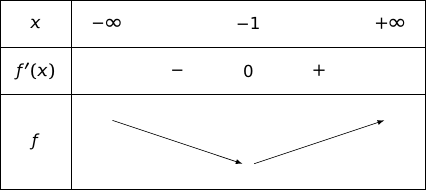
3. En déduire les variations de la fonction .
Pour tout , , donc le signe de est le même que celui de , ce qui donne le tableau de variations :
PARTIE B
Dans le repère orthogonal ci-dessous trois courbes et ont été représentées.
L'une de ces courbes représente la fonction , une autre représente sa dérivée et une troisième représente sa dérivée seconde.
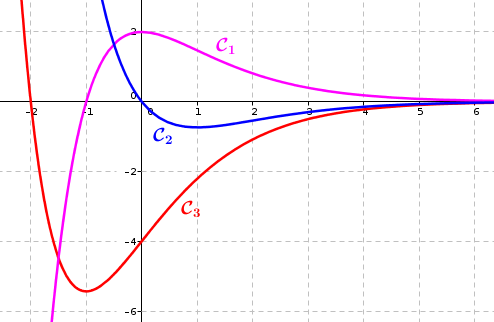
Expliquer comment ces représentations graphiques permettent de déterminer la convexité de la fonction .
Indiquer un intervalle sur lequel la fonction est convexe.
Au vu des variations la courbe représentative de ne peut être que ou .
Si la courbe représentative de est , vu le signe des fonctions représentées par et , aucune ne peut être la dérivée, donc ce n'est pas qui est la courbe représentative de et c'est .
Il en découle en observant les signes que est la courbe représentative de et que est la courbe représentative de .
On remarque que la dérivée seconde est positive sur et que la fonction est convexe sur cet intervalle.
