Sujet et corrigé de l'exercice 4 du bac ES de maths d'avril 2015 à Pondichéry
Cacher les corrigés
Une entreprise produit et vend des composants électroniques.
Sa capacité mensuelle de production est comprise entre 1 000 et 30 000 pièces.
On suppose que toute la production est commercialisée.
PARTIE A
On donne ci-dessous et les représentations graphiques respectives des fonctions recette et coût sur l'intervalle .
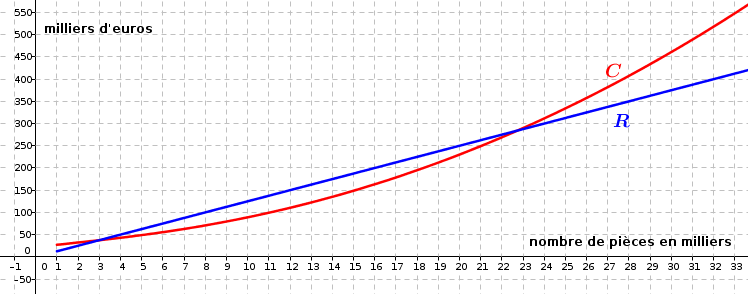
Par lecture graphique, donner une estimation des valeurs demandées.
1. Quel est le coût de production de 21 000 pièces ?
250 000 euros.
2. Pour quelles quantités de pièces produites l'entreprise réalise-t-elle un bénéfice ?
Entre 3 000 pièces et 23 000 pièces environ.
3. Pour quel nombre de pièces produites le bénéfice est-il maximal ?
Autour de 13 000 pièces.
PARTIE B
Le bénéfice en milliers d'euros, réalisé pour la production et la vente de milliers de pièces, est donné sur l'intervalle par
1. Montrer que , où est la dérivée de sur l'intervalle .
Il s'agit de dériver :
d'une part et
d'autre part.
Pour la première « partie » on obtient directement :
Pour la seconde partie c'est de la forme avec :
;
;
La dérivée est :
Finalement :
2. On admet que , où est la dérivée seconde de sur l'intervalle .
Justifier le tableau de variation ci-dessous de la fonction dérivée sur l'intervalle .
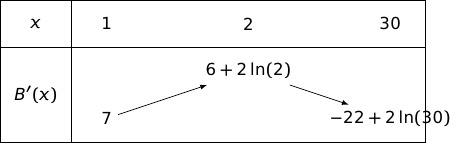
Pour , on étudie le signe de pour obtenir les variations de :
, donc est croissante sur .
, donc est décroissante sur .
Calculs des images :
3.a. Montrer que l'équation admet une unique solution sur l'intervalle .
Sur , le minimum de est 7, donc l'équation ne peut pas avoir de solution.
Sur , la fonction est continue et strictement décroissante avec :
où .
Du coup et d'après le théorème de la valeur intermédiaire, l'équation admet une unique solution dans .
b. Donner une valeur approchée au millième de la valeur de .
En utilisant la calculette, avec, par exemple, la méthode de balayage on trouve :
4. En déduire le signe de sur l'intervalle , et donner le tableau de variation de la fonction bénéfice sur ce même intervalle.
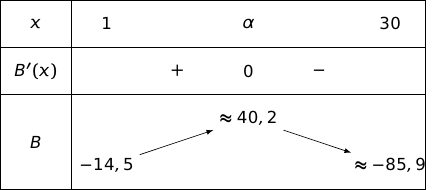
5. Quel est le nombre de pièces à produire, à l'unité près, pour que l'entreprise réalise un bénéfice maximal ?
Quel est ce bénéfice maximal (arrondi au millier d'euros) ?
D'après l'étude précédente, le bénéfice maximal est atteint pour environ 13 153 pièces et il vaut environ 40 200 euros.
