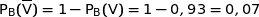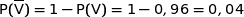Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2016 en Amérique du nord
Cacher les corrigés
Une entreprise fabrique des billes en bois sphériques grâce à deux machines de production A et B. L'entreprise considère qu'une bille peut être vendue uniquement lorsque son diamètre est compris entre 0,9 cm et 1,1 cm.
Les trois parties sont indépendantes.
Partie A
Une étude du fonctionnement des machines a permis d'établir les résultats suivants :
96 % de la production journalière est vendable.
La machine A fournit 60 % de la production journalière.
La proportion de billes vendables parmi la production de la machine A est 98 %.
On choisit une bille au hasard dans la production d'un jour donné. On définit les événements suivants :
A : « la bille a été fabriquée par la machine A »;
B : « la bille a été fabriquée par la machine B »;
V : « la bille est vendable ».
1. Déterminer la probabilité que la bille choisie soit vendable et provienne de la machine A.
On peut représenter la situation par un arbre :
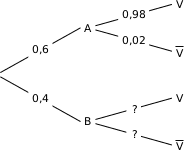
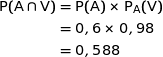
2. Justifier que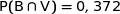 
et en déduire la probabilité que la bille choisie soit vendable
sachant qu'elle provient de la machine B.
Les événements A et B forment une partition de l'univers associé à l'expérience aléatoire. D'après la formule des probabilités totales :
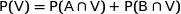
or nous savons que :
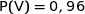(énoncé)
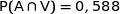(question 1)
donc
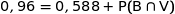
et
.
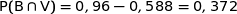Maintenant on calcule :
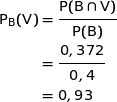
3. Un technicien affirme que 70 % des billes non vendables proviennent de la machine B.
A-t-il raison ?
On calcule :
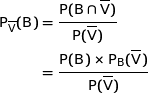
avec :
Donc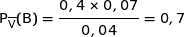 
Donc le technicien a raison.
Partie B
Dans cette partie, on s'intéresse au diamètre, exprimé en cm, des billes produites par les machines A et B.
1. Une étude statistique conduit à modéliser le diamètre d'une bille prélevée au hasard
dans la production de la machine B par une variable aléatoir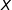e 
qui suit une loi normale
d'espérance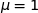 
et d'écart-type 
.
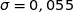Vérifier que la probabilité qu'une bille produite par la machine B soit vendable est bien celle trouvée dans la partie A, au centième près.
En utilisant la calculette on obtient :
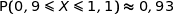
Dans la partie A on a vu que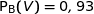 
.
Le résultat obtenu avec la variable aléatoire 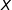correspond bien.
2. De la même façon, le diamètre d'une bille prélevée au hasard dans la production de
la machine A est modélisé à l'aide d'une variable aléatoir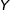e 
qui suit une loi normale
d'espérance 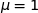et d'écart-type 
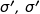étant un réel strictement positif.
Sachant que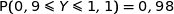 
, déterminer une valeur approchée au millième
de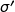 
.
Pour répondre à cette question on se ramène à la loi normale centrée réduite.
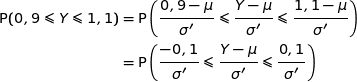
où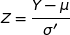 
suit la loi normale centrée réduite, c'est à dire qu'on a :
.
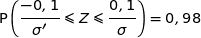Faisons un petit dessin :
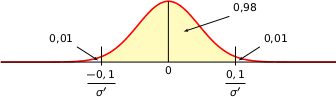
En utilisant la calculette et la fonction inverse normale avec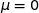 
et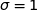 
et en entrée 0,99 on obtient 2,326 environ.
Note : Sur casio, régler « tail » à « left » ou alors entrer 0,98 et régler « tail » à « center ».
Dans tous les cas on en déduit que :
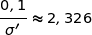et donc 
.
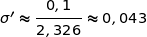Partie C
Les billes vendables passent ensuite dans une machine qui les teinte de manière aléatoire et équiprobable en blanc, noir, bleu, jaune ou rouge. Après avoir été mélangées, les billes sont conditionnées en sachets. La quantité produite est suffisamment importante pour que le remplissage d'un sachet puisse être assimilé à un tirage successif avec remise de billes dans la production journalière.
Une étude de consommation montre que les enfants sont particulièrement attirés par les billes de couleur noire.
1. Dans cette question seulement, les sachets sont tous composés de 40 billes.
a) On choisit au hasard un sachet de billes. Déterminer la probabilité que le sachet
choisi contienne exactement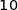 
billes noires. On arrondira le résultat à 
.
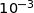On peut assimiler le remplissage d'un sachet à la répétition de 40 expériences de Bernoulli identiques et indépendantes dont la loi est :
où N est l'événement « la bille est noire ».
Soit 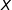la variable aléatoire qui compte le nombre de billes noires au moment du remplissage du sachet, alors 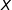suit la loi binomiale de paramètres 
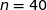et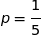 
.
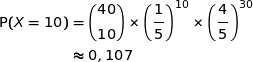
b) Dans un sachet de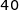 
billes, on a compté 
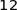billes noires. Ce constat permet-t-il
de remettre en cause le réglage de la machine qui teinte les billes ?
La proportion théorique de billes noires est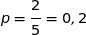 
.
Un sachet de 40 billes est un échantillon de taille .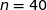
Nous avons ainsi :
; 
; 
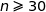
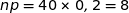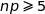
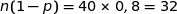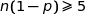
Il est donc possible d'utiliser l'intervalle de fluctuation asymptotique à 95 % associé à la situation :
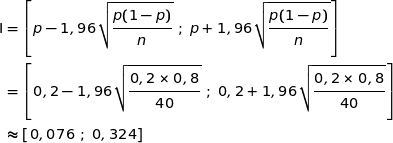
La fréquence observée de billes noires dans l'échantillon est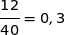 
, or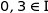 
, donc au vu de cela on ne peut pas remettre en cause le réglage de la machine.
2. Si l'entreprise souhaite que la probabilité d'obtenir au moins une bille noire dans un sachet soit supérieure ou égale à 99 %, quel nombre minimal de billes chaque sachet doit-il contenir pour atteindre cet objectif ?
En reprenant les notations de la question 1.a., soit 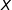la variable aléatoire qui compte le nombre de billes noires dans un sachet de 
billes. Alors 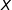suit la loi binomiale de paramètres et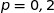 
.
On cherche tel que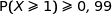 
.
Il s'agit maintenant de résoudre l'inéquation :
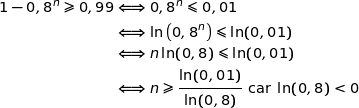
où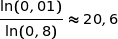 
.
Donc pour atteindre l'objectif fixé chaque sachet doit contenir au moins 21 billes.
