Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2016 en Amérique du nord
Cacher les corrigés
Le plan complexe est rapporté à un repère orthonormé direct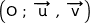 
.
On considère le point A d'affixe 4, le point B d'affixe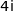 
et les points C et D tels que ABCD est un carré de centre O.
Pour tout entier naturel non nul 
, on appelle 
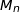le point d'affixe 
.
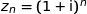1. Ecrire le nombre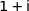 
sous forme exponentielle.
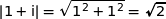
Par suite :
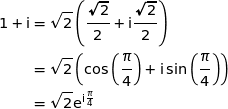
2. Montrer qu'il existe un entier naturel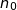 
, que l'on précisera, tel que, pour tout entier
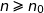, le point 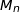est à l'extérieur du carré ABCD.
Pour tout entier naturel non nul :
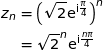
Un petit dessin :
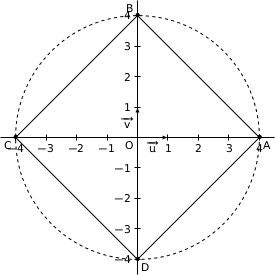
Remarquons déjà que le carré est inscrit dans le cercle de centre O et de rayon 4 ; donc pour tout entier tel que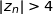 
, le point 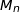est à l'extérieur du carré.
Pour entier naturel non nul :
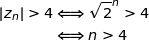
On peut donc prendre provisoirement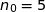 
.
Pour déterminer 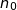« au plus juste » il y a au plus 4 cas à étudier.
Si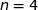 
; 
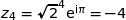
or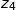 
est l'affixe de C, par conséquent 
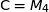n'est pas à l'extérieur du carré.
Il s'ensuit que .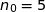
