Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2015 dans les centres étrangers
Cacher les corrigés
Tous les résultats demandés dans cet exercice seront arrondis au millème.
Les parties A, B et C sont indépendantes.
Un fournisseur produit deux sortes de cadenas. Les uns sont « premier prix », et les autres sont « haut de gramme ».
Un magasin de bricolage dispose d'un stock de cadenas provenant de ce fournisseur ; ce stock comprend un grand nombre de cadenas de chaque type.
Partie A
1. Le fournisseur affirme que, parmi les cadenas « haut de gamme », il n'y a pas plus de 3 % de cadenas défectueux dans sa production. Le responsable du magasin de bricolage désire vérifier la validité de cette affirmation dans son stock ; à cet effet, il prélève un échantillon aléatoire de 500 cadenas « haut de gamme », et en trouve 19 qui sont défectueux.
Ce contrôle remet-il en cause le fait que le stock ne comprenne pas plus de 3 % de cadenas défectueux ?
On pourra pour cela utiliser un intervalle de fluctuation asymptotique au seuil de 95 %.
L'intervalle de fluctuation asymptotique à 95 % à considérer est le suivant :
avec et .
On vérifie que les conditions usuelles d'utilisation de cet intervalle sont vérifiées :
; donc
; donc
; donc
L'intervalle de fluctuation est :
soit
La proportion de cadenas défectueux observée dans l'échantillon est :
Or , donc ce contrôle ne remet pas en cause le fait que le stock ne comprenne pas plus de 3 % de cadenas défectueux.
2. Le responsable du magasin souhaite estimer la proportion de cadenas défectueux dans son stock de cadenas « premier prix ». Pour cela il prélève un échantillon aléatoire de 500 cadenas « premier prix », parmi lesquels 39 se révèlent défectueux.
Donner un intervalle de confiance de cette proportion au niveau de confiance 95 %.
L'intervalle de confiance au seuil de 95 % est donné par :
avec ici et .
On vérifie que les conditions d'utilisation sont vérifiées :
; donc ,
; donc ,
; donc
et on obtient :
soit
Partie B
D'après une étude statistique faite sur plusieurs mois, on admet que le nombre de cadenas « premier prix » vendus par mois dans le magasin de bricolage peut être modélisé par une variable aléatoire qui suit la loi normale de moyenne et d'écart-type .
1. Calculer .
En remarquant que et on a :
.
(Résultat connu).
2. Le responsable du magasin veut connaître le nombre de cadenas « premier prix » qu'il doit avoir en stock en début de mois, pour que la probabilité d'être en rupture de stock en cours de mois soit inférieure à 0,05. On ne réalimente pas le stock en cours de mois.
Déterminer la plus petite valeur de l'entier remplissant cette condition.
Il s'agit de chercher tel que :
En utilisant la calculette on trouve que .
(Inverse normale de 0,95 ; avec tail à left pour les calculatrices CASIO).
La fonction est décroissante, donc le plus petit entier remplissant la condition est 792.
Partie C
On admet maintenant que, dans le magasin :
80 % des cadenas proposés à la vente sont « premier prix », les autres « haut de gamme » ;
3 % des cadenas « haut de gamme » sont défectueux ;
7 % des cadenas sont défectueux.
On prélève au hasard un cadenas dans le magasin. On note :
la probabilité qu'un cadenas « premier prix » soit défecteux ;
H l'événement : « le cadenas prélevé est haut de gamme » :
D l'événement : « le cadenas prélevé est défectueux ».
1. Représenter la situation à l'aide d'un arbre pondéré.
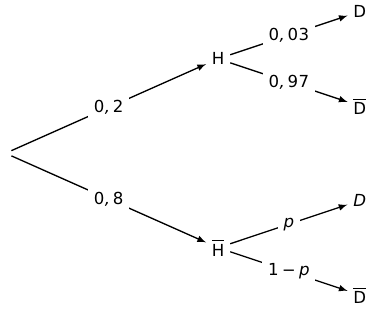
2. Exprimer en fonction de la probabilité . En déduire la valeur du réel .
Le résultat est-il cohérent avec celui de la question A-2 ?
Les événements H et forment une partition de l'univers donc d'après la formule des probabilités totales :
Comme il vient :
Ce résultat est cohérent avec la question A-2, car 0,08 se trouve dans la fourchette donnée par l'intervalle de confiance.
3. Le cadenas prélevé est en bon état. Déterminer la probabilité que ce soit un cadenas « haut de gamme ».
