Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2015 dans les centres étrangers
Cacher les corrigés
Pour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
1. Dans le plan muni d'un repère orthonormé, on note S l'ensemble des points M dont l'affixe vérifie les deux conditions :
et
Sur la figure ci-dessous, on a représenté le cercle de centre le point de coordonnées et de rayon 2, et la droite d'équation .
Cette droite coupe le cercle en deux points A et B.
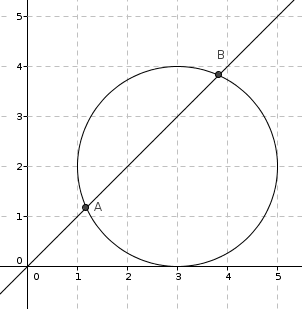
Affirmation 1 : l'ensemble S est le segment [AB].
La relation caractérise les points équidistants des points U d'affixe 1 et V d'affixe , c'est à dire les points de la médiatrice de [UV] qui n'est autre que la droite d'équation .
La relation caractérise les points dont la distance au point de coordonnées est inférieure ou égale à 2, c'est à dire les points du disque considéré dans la question (frontière incluse).
Les points de la droite d'équation qui se trouvent également dans le disque (frontière incluse) sont les points du segment [AB].
L'affirmation est vraie.
2. Affirmation 2 : le nombre complexe est un réel.
On commence par déterminer la forme exponentielle du nombre complexe :
Du coup en factorisant par le module obtenu :
On cherche alors tel que :
On peut prendre et on a :
On a alors :
Ainsi un argument du nombre est :
Modulo , un argument est donc , donc le nombre considéré est imaginaire pur et non réel.
L'affirmation est fausse.
Pour les questions 3 et 4, on considère les points :
, et
dont les coordonnées sont définies dans un repère orthonormé de l'espace.
3. Affirmation 3: une représentation paramétrique de la droite (EF) est donnée par :
On « regarde » si les points E et F appartiennent à la droite dont on nous donne une représentation paramétrique.
Pour le point E : , donc E appartient à la droite.
Pour le point F : , donc F appartient à la droite.
Ainsi la droite dont on nous une représentation paramétrique passe par E et F, c'est donc la droite (EF).
L'affirmation est vraie.
4. Affirmation 4 : une mesure en degré de l'angle géométrique , arrondie au degré est 50°.
On commence par déterminer les coordonnées des vecteurs et :
soit
soit
On utilise une relation vue en première avec le produit scalaire dans le plan et encore valable dans l'espace :
Comme on est en repère orthonormé, le produit scalaire s'obtient par :
De plus :
Donc
Et avec la calculette on trouve .
L'affirmation est vraie.
