Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2015 dans les centres étrangers
Cacher les corrigés
Soit un nombre réel fixé non nul.
Le but de cet exercice est d'étudier la suite définie par :
, et pour tout de , .
On remarquera que cette égalité peut aussi s'écrire :
1. Soit la fonction définie pour tout réel par : .
a. Calculer et prouver que, pour tout réel : .
La fonction est dérivable sur et pour tout réel :
En partant de l'expression donnée dans l'énoncé, il vient :
b. Déterminer les variations de la fonction et donner la valeur de son minimum.
Pour tout réel : et comme , le signe de est le même que celui de , on résout alors :
De même on a :
On peut alors dresser le tableau de variations :
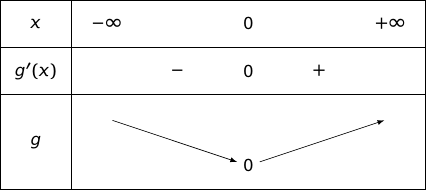
Du coup admet un minimum en qui vaut .
c. En remarquant que , étudier le sens de variation de la suite .
Pour tout entier naturel :
Or, pour tout , (minimum vu à la question précédente) et en particulier .
Ainsi, pour tout entier naturel , ce qui montre que est croissante.
2. Dans cette question, on suppose que .
a. Démontrer par récurrence que, pour tout entier naturel , .
Initialisation au rang 0
Comme et qu'on suppose que , on a , ce qui montre que la propriété est vraie au rang 0.
Hérédité
Supposons que la propriété est vraie à un rang : .
On veut montrer, qu'alors : .
On sait que :
Comme , le signe de est le même que celui de .
Il s'agit alors d'étudier le signe de cette dernière expression sous l'hypothèse que (hypothèse de récurrence).
Du coup, et la propriété est héréditaire.
On a ainsi notre propriété qui est vraie au rang 0 et qui est héréditaire, donc elle est vraie pour tout entier naturel .
b. Déduire des questions précédentes que la suite est convergente.
La suite :
est croissante (question 1.c.)
est majorée par 0 (question 2.b.)
donc d'après le théorème de convergence monotone on peut dire que la suite est convergente.
c. Dans le cas où vaut 0, donner la limite de la suite .
Si ; et comme la suite est croissante et majorée par 0, elle ne peut être que constante et égale à 0.
Donc .
3. Dans cette question, on suppose que .
La suite étant croissante, la question 1. permet d'affirmer que, pour tout entier naturel , .
a. Démontrer que, pour tout entier naturel , on a : .
On sait que pour tout entier naturel : .
De plus est croissante sur (étude de la fonction à la question 1).
Du coup pour tout entier naturel : .
Et comme on a bien : .
b. Démontrer par récurrence que, pour tout entier naturel , on a :
Initialisation au rang 0
et .
Donc (il y a égalité).
Ainsi la propriété est vrai au rang 0.
Hérédité
On suppose qu'à un rang on a : .
On montre, qu'alors : .
Pour cela exploitons le résultat de la question a. :
Ensuite nous faisons intervenir l'hypothèse de récurrence :
Donc la propriété est héréditaire.
Ainsi notre propriété est vraie au rang 0 ; elle est héréditaire, donc elle est vraie pour tout entier naturel .
c. Déterminer la limite de la suite .
Nous avons et d'après l'étude de la fonction faite à la question 1, nous avons également .
Du coup : et en ajoutant :
Comme , par comparaison on a : .
4. Dans cette question, on prend .
L'algorithme suivant a pour but de déterminer le plus petit entier tel que où M désigne un réel positif. Cet algorithme est incomplet.
| Variables : | est un entier, et M sont deux réels |
| Initialisation : | prend la valeur 0,02 |
| prend la valeur 0 | |
| Saisir la valeur de M | |
| Traitement : | Tant que ...... |
| ...... | |
| ...... | |
| Fin tant que | |
| Sortie : | Afficher |
a. Sur la copie, recopier la partie « Traitement » en la complétant.
| Variables : | est un entier, et M sont deux réels |
| Initialisation : | prend la valeur 0,02 |
| prend la valeur 0 | |
| Saisir la valeur de M | |
| Traitement : | Tant que |
| prend la valeur | |
| prend la valeur | |
| Fin tant que | |
| Sortie : | Afficher |
b. A l'aide de la calculatrice, déterminer la valeur que cet algorithme affichera si .
Avec la calculette on trouve que l'algorithme affiche 36.
