Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2015 dans les centres étrangers
Cacher les corrigés
Les parties A et B sont indépendantes.
Le fabricant de cadenas de la marque « K » désire imprimer un logo pour son entreprise.
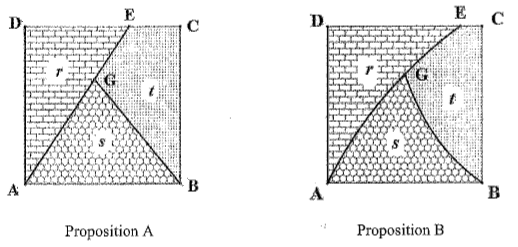
Ce logo a la forme d'une lettre majuscule K stylisée, inscrite dans un carré ABCD, de côté une unité de longueur, et respectant les conditions C1 et C2 suivantes.
Condition C1 : la lettre K doit être constituée de trois lignes :
- une des lignes est le segment [AD] ;
- une deuxième ligne a pour extrémités le point A et un point E du segment [DC] ;
- la troisième ligne a pour extrémité le point B et un point G situé sur la deuxième ligne.
Condition C2 : l'aire de chacune des trois surfaces délimitées par les trois lignes dessinées dans le carré doit être comprise entre 0,3 et 0,4, l'unité d'aire étant celle du carrée. Ces aires sont notées , , sur les figures ci-après.
Un atelier de design propose deux dessins possibles, représentés ci-dessous.
Pour mener les études qui suivent, on se place dans le repère orthonormé .
Partie A : étude de la proposition A
Dans cette proposition les trois lignes sont des segments et les trois aires sont égales :
.
Déterminer les coordonnées des points E et G.
On commence par déterminer la position de E pour que .
Comme ADE est un triangle rectangle et étant donné la configuration on a :
Donc et
Du coup
Pour le point G ; on considère le triangle AGB, son aire est :
Donc et .
Pour déterminer l'abscisse de G on utilise le fait que .
La droite (AE) a pour équation et comme elle passe par E :
, soit (AE) : .
Les coordonnées de G vérifient l'équation :
Donc
Partie B : étude de la proposition B
Cette proposition est caractérisée par les deux modalités suivantes :
la ligne d'extrémités A et E est une portion de la représentation graphique de la fonction définie pour tout réel par : ;
la ligne d'extrémités B et G est une portion de la représentation graphique de la fonction définie pour tout réel par : , où est un réel positif qui sera déterminé.
1.a. Déterminer l'abscisse du point E.
Le point E a pour ordonnée 1 et il est situé sur la courbe représentative de la fonction , donc , ce qui donne l'équation :
Cette équation est définie pour tout réel tel que et sous cette condition nous avons les équivalences :
Comme ; est bien la solution de l'équation considérée et
b. Déterminer la valeur du réel , sachant que l'abscisse du point G est égale à 0,5.
Comme G appartient à la courbe représentative de sont ordonnée est :
.
Donc
Le point G appartient également à la courbe représentative de donc on a également :
2.a. Démontrer que la fonction admet pour primitive la fonction définie pour tout réel par :
La fonction est dérivable sur et on a :
avec :
;
;
Ce qui montre que est bien une primitive de sur .
b. Démontrer que .
est l'aire du domaine délimité par :
la droite d'équation ;
la courbe représentative de ;
la droite d'équation et la droite d'équation
Compte tenu de la configuration cette aire s'exprime par :
3. Déterminer une primitive de la fonction sur l'intervalle .
Pour tout , on a :
Du coup cette fonction admet des primitives sur et on a :
4. On admet que les résultats précédents permettent d'établir que :
La proposition B remplit-elle les conditions imposées par le fabricant ?
La condition C1 des 3 lignes est respectée.
Pour la condition C2 on a :
Du coup :
On a donc bien les 3 aires qui sont comprises entre 0,3 et 0,4 u.a., donc la proposition B remplit les conditions imposées par le fabricant.
