Sujet et corrigé de l'exercice 1 du bac S de maths de mai 2015 au liban
Cacher les corrigés
ABCDEFGH est un cube.
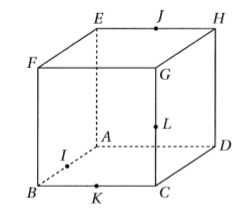
I est le milieu du segment [AB], J est le milieu du segment [EH], K est le milieu du segment [BC] et L est le milieu du segment [CG].
On munit l'espace du repère orthonormé .
1.a. Démontrer que la droite (FD) est orthogonale au plan (IJK).
Pour montrer que la droite (FD) est orthogonale au plan (IJK), on montre que est orthogonal à deux vecteurs non colinéaires de (IJK), comme par exemple et .
Dans le repère orthonormé considéré nous avons : et du coup :
soit
Nous avons : ; et et :
soit
soit
, donc est orthogonal à
, donc est orthogonal à
Ainsi est orthogonal à deux vecteurs non colinéaires du plan (IJK), cela montre que la droite (FD) est orthogonale à ce plan.
b. En déduire une équation cartésienne du plan (IJK).
D'après la question précédente, on a qui est un vecteur normal au plan (IJK) et donc ce plan admet une équation cartésienne de la forme :
Comme le point I appartient au plan on a, en remplaçant les coordonnées de I dans l'équation :
Finalement une équation cartésienne de (IJK) est : .
2. Déterminer une représentation paramétrique de la droite (FD).
En utilisant le point D et le vecteur , on a directement :
avec qui décrit .
3. Soit M le point d'intersection de la droite (FD) et du plan (IJK).
Déterminer les coordonnées du point M.
En utilisant l'équation cartésienne du plan et la représentation paramétrique de la droite nous formons le système :
Donc le plan et la droite sont sécants au point
4. Déterminer la nature du triangle IJK et calculer son aire.
Nous commençons par calculer les longueurs des 3 côtés du triangle.
On remarque tout de suite que : , ce qui montre que IJK est rectangle en I, comme , il n'est pas isocèle.
Son aire est :
5. Calculer le volume du tétraèdre FIJK.
Le tétraèdre a pour base IJK et pour hauteur [FM] car la droite (FD)=(FM) est orthogonale au plan (IJK).
En utilisant la formule qui donne le volume du tétraèdre de base IJK et de hauteur [FM] nous avons :
6. Les droites (IJ) et (KL) sont-elles sécantes ?
Nous avons : et soit
Une représentation paramétrique de (IJ) est :
Une représentation paramétrique de (KL) est :
Pour savoir si les droites sont sécantes on cherche leur point d'intersection éventuel en résolvant le système :
Ainsi le système admet une unique solution, donc les droites sont sécantes.
AUTRE SOLUTION (merci à Tr. D.)
On a et les coordonnées de ce point vérifient l'équation cartésienne du plan (IJK) trouvé à la question 1.b :
Du coup, L appartient au plan (IJK) et les points I, J, K et L sont coplanaires.
D'autre part nous avons : et soit
On remarque que les coordonnées de ne sont pas proportionnelles à celles de , donc les vecteurs et ne sont pas colinéaires et du coup les droites (IJ) et (KL) ne sont pas parallèles et comme (KL) et (IJ) sont coplanaires cela entraîne qu'elles sont sécantes.
