Sujet et corrigé de l'exercice 3 du bac S de maths de mai 2015 au Liban
Cacher les corrigés
On considère la courbe d'équation , tracée ci-dessous.
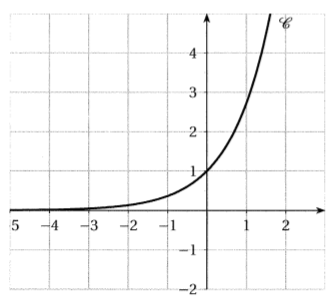
Pour tout réel strictement positif, on note la droite d'équation .
1. Dans cette question, on choisit .
Démontrer que la droite , d'équation , est tangente à la courbe en son point d'abscisse 1.
Soit la fonction définie sur par .
Alors
L'équation de la tangente au point d'abscisse 1 à la courbe est :
soit ; ce qui donne .
2. Conjecturer, selon les valeurs prises par le réel strictement positif , le nombre de points d'intersection de la courbe et de la droite .
En faisant tourner la règle autour de l'origine du repère on conjecture que le nombre de points d'intersection de et est :
0 lorsque ,
1 lorsque ,
2 lorsque .
3. Démontrer cette conjecture.
Pour , il s'agit de déterminer le nombre de solutions de l'équation :
Pour cela on étudie la fonction définie sur par :
Cette fonction est dérivable sur et on a :
(on n'oublie pas que ).
De la même façon :
et .
On a donc le tableau de variations :
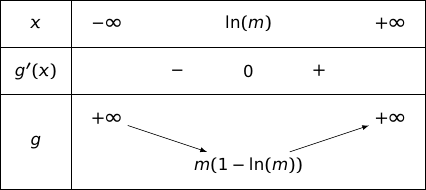
Limite en
;
Donc par somme,
Limite en
On a une forme indéterminée et on écrit :
(inverse de la limite connue : )
En multipliant par et par différence :
Finalement par produit,
Minimum
Le nombre de solutions de l'équation va dépendre du signe de et comme , c'est le signe de qu'il faut étudier, on résout donc :
De même :
et .
Du coup on a les trois cas suivants :
; alors le minimum de sur est strictement positif, donc l'équation n'a pas de solution.
et n'ont pas de point d'intersection.
; alors le minimum de sur est 0 et l'équation a une unique solution.
et ont un unique point d'intersection.
; alors le minimum de sur est strictement négatif ; en appliquant le théorème de la valeur intermédiaire sur chacun des intervalles et , on montre que a deux solutions sur .
et ont deux points d'intersection.
On montre ainsi les conjectures faites à la question 2.
