Sujet et corrigé de l'exercice 4 du bac S de maths de mai 2015 au Liban
Cacher les corrigés
En prévision d'une élection entre deux candidats A et B, un institut de sondage recueille les intentions de vote de futurs électeurs.
Parmi les 1 200 personnes qui ont répondu au sondage, 47 % affirment vouloir voter pour le candidat A et les autres pour le candidat B.
Compte-tenu du profil des candidats, l'institut de sondage estime que 10 % des personnes déclarant vouloir voter pour le candidat A ne disent pas la vérité et votent en réalité pour le candidat B, tandis que 20 % des personnes déclarant vouloir voter pour le candidat B ne disent pas la vérité et votent en réalité pour le candidat A.
On choisit au hasard une personne ayant répondu au sondage et on note :
A l'évènement « La personne interrogée affirme vouloir voter pour le candidat A »,
B l'évènement « La personne interrogée affirme vouloir voter pour le candidat B »,
V l'évènement « La personne interrogée dit la vérité ».
1. Construire un arbre de probabilités traduisant la situation.
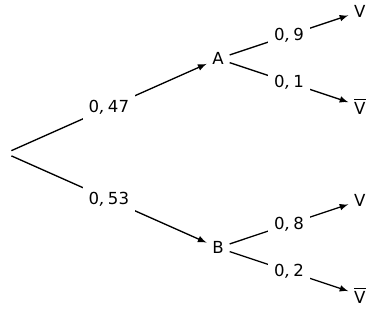
2.a. Calculer la probabilité que la personne interrogée dise la vérité.
Les événements A et B partitionnent l'univers donc d'après la formule des probabilités totales :
b. Sachant que la personne interrogée dit la vérité, calculer la probabilité qu'elle affirme vouloir voter pour le candidat A.
3. Démontrer que la probabilité que la personne choisie vote effectivement pour le candidat A est 0,529.
La personne choisie vote pour le candidat A dans deux cas :
la personne dit voter pour A et elle dit la vérité,
la personne dit voter pour B et elle ment.
On calcule donc :
4. L'institut de sondage publie alors les résultats suivants :
| 52,9 % des électeurs voteraient pour le candidat A. |
| estimation après redressement, fondée sur un sondage d'un |
| échantillon représentatif de 1 200 personnes. |
Au seuil de confiance de 95 %, le candidat A peut-il croire en sa victoire ?
L'intervalle de confiance au seuil de 95 % est donné par :
avec ici et .
On vérifie que les conditions d'utilisation sont vérifiées :
; donc ,
; donc ,
; donc
et on obtient :
soit
Au seuil de 95 %, avec la fourchette donnée par l'intervalle de confiance, le candidat A peut croire en sa victoire.
5. Pour effectuer ce sondage, l'institut a réalisé une enquête téléphonique à raison de 10 communications par demi-heure. La probabilité qu'une personne contactée accepte de répondre à cette enquête est 0,4.
L'institut de sondage souhaite obtenir un échantillon de 1 200 réponses.
Quel temps moyen, exprimé en heures, l'institut doit-il prévoir pour parvenir à cet objectif ?
En une demi-heure, on répète 10 expériences de Bernoulli indépendantes dont la probabilité du succès (la personne accepte de répondre) est 0,4.
La variable aléatoire qui compte le nombre de personnes qui répondent au cours de la demi-heure suit la loi binomiale de paramètres 10 et 0,4.
On a
Cela signifie que l'institut peut espérer obtenir 4 réponses par demi-heure.
Du coup l'institut doit prévoir en moyenne, demis-heures soit 150 heures.
