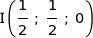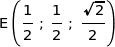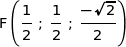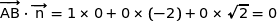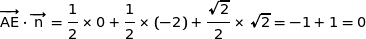Sujet et corrigé de l'exercice 1 du bac S de maths de mai 2016 au Liban
Cacher les corrigés
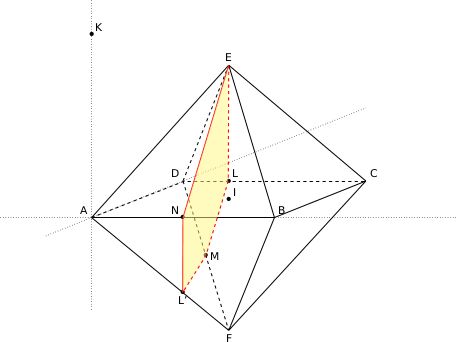
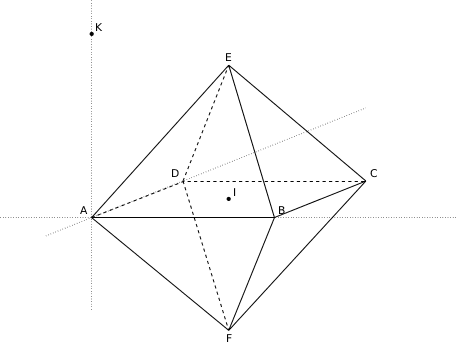
On considère un solide ADECBF constitué de deux pyramides identiques ayant pour base commune le carré ABCD de centre I. Une représentation en perspective de ce solide est donnée ci-dessous. Toutes les arêtes sont de longueur 1.
L'espace est rapporté au repère orthonormé
.
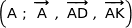1.
a) Montrer que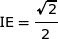 
. En déduire les coordonnées des points I, E et F.
La diagonale du carré ABCD de côté 1 est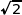 
, donc 
.
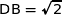On travaille dans le triangle DEB. Comme toutes les arêtes du solide sont de longueur 1, DBE est un triangle isocèle en E.
De plus I étant le milieu du carré ABCD, I est au milieu du segment [DB].
Par suite nous sommes dans la situation suivante :
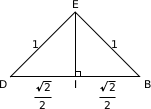
Le triangle IBE est rectangle en I et d'après la propriété de Pythagore :
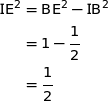
Donc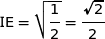 
.
Coordonnées des points :
b) Montrer que le vecteur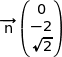 
est normal au plan (ABE).
Deux vecteurs non colinéaires du plan (ABE) sont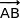 
et 
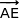dont les coordonnées sont les mêmes que B et E soit :
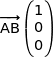et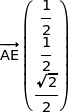 
Ainsi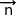 
est orthogonal a deux vecteurs non colinéaires du plan (ABE) ce qui prouve que 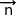est normal à ce plan.
c) Déterminer une équation cartésienne du plan (ABE).
Le vecteur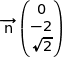 
est normal au plan (ABE) donc une équation cartésienne de ce plan est la forme :
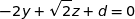
Le plan passe par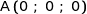 
, donc 
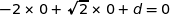soit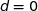 
.
Finalement une équation cartésienne de (ABE) est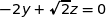 
.
2. On nomme M le milieu du segment [DF] et N celui du segment [AB].
a) Démontrer que les plans (FDC) et (ABE) sont parallèles.
Nous avons déjà la droite (AB) du plan (ABE) qui est parallèle à la droite (DC) du plan (FDC) (car ABCD est un carré).
Montrons que (FC) est parallèle à (AE).
Nous avons déjà
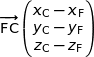
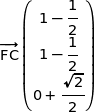soit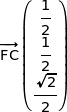 
On a donc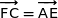 
, donc (FC) et (AE) sont bien parallèles.
Nous avons ainsi les deux droites sécantes (AB) et (AE) du plan (ABE) qui sont parallèles aux deux droites sécantes (DC) et (FC) du plan (FDC) ce qui prouve que les deux plans en question sont parallèles.
b) Déterminer l'intersection des plans (EMN) et (FDC).
Remarquons déjà que les plans en question ne sont pas confondus et qu'ils sont sécants puisqu'ils ont le point M en commun. Par suite l'intersection de ces deux plans est une droite qui passe par M.
Les plans (ABE) et (FDC) sont parallèles, le plan (EMN) coupe le plan (ABE) selon la droite (EN) donc il coupe le plan (FDC) selon une droite parallèle à (EN). Ainsi l'intersection de (EMN) et (FDC) est la droite parallèle à (EN) qui passe par M.
c) Construire la section du solide ADECBF par le plan (EMN).
Section du solide par le plan (EMN).
On notera que les droites (EL) et (NL') sont parallèles car le plan (EMN) coupe les deux plans parallèles (DEC) et (ABF) selon deux droites parallèles.
