Sujet et corrigé de l'exercice 2 du bac S de maths de mai 2016 au Liban
Cacher les corrigés
Sur un court de tennis, un lance-balle permet à un joueur de s'entraîner seul. Cet appareil envoie des balles une par une à une cadence régulière. Le joueur frappe alors la balle puis la balle suivante arrive.
Suivant le manuel du constructeur, le lance-balle envoie au hasard la balle à droite ou à gauche avec la même probabilité.
Dans tout l'exercice, on arrondira les résultats à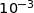 
près.
Partie A
Le joueur s'apprête à recevoir une série de 20 balles.
1. Quelle est la probabilité que le lance-balle envoie 10 balles à droite ?
Considérons le lancer d'une balle. Alors la loi de probabilité associée est :
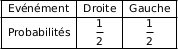
On effectue 20 répétitions indépendantes de cette même expérience aléatoire. La variable aléatoire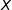 
qui compte le nombre de balles que la machine envoie à droite suit la loi binomiale de paramètres 
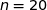et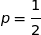 
.
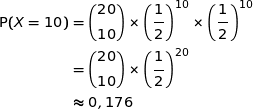
2. Quelle est la probabilité que le lance-balle envoie entre 5 et 10 balles à droite ?
Avec les mêmes notations qu'à la question précédente :
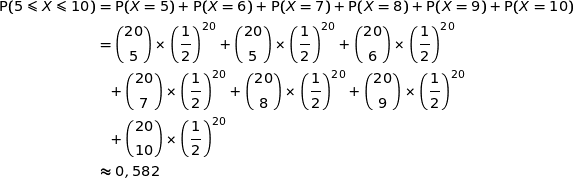
Partie B
Le lance-balle est équipé d'un réservoir pouvant contenir 100 balles. Sur une séquence de 100 lancers, 42 balles ont été lancées à droite.
Le joueur doute alors du bon fonctionnement de l'appareil. Ses doutes sont-ils justifiés ?
Pour répondre à cette question on peut utiliser un intervalle de fluctuation asymptotique à 95 %.
On remarque déjà que les conditions usuelles d'utilisation sont vérifiées :
La taille de l'échantillon est
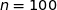; donc 
;
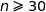La proportion « théorique » de balles à droites est
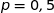, du coup 
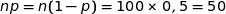et donc 
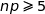et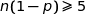 
.
L'intervalle de fluctuation asymptotique à 95 % est donné par la formule :
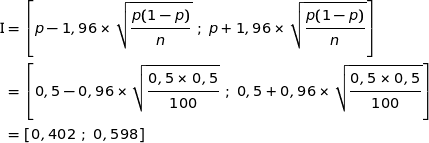
La fréquence observée dans l'échantillon es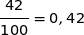t 
et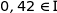 
.
Au vu de cet échantillon on ne peut pas dire que les doutes du joueur sont justifiés.
Partie C
Pour augmenter la difficulté le joueur paramètre le lance-balle de façon à donner un effet aux balles lancées. Elles peuvent être soit « liftées » soit « coupées ». La probabilité que le lance-balle envoie une balle à droite est toujours égale à la probabilité que le lance-balle envoie une balle à gauche.
Les réglages de l'appareil permettent d'affirmer que :
la probabilité que le lance-balle envoie une balle liftée à droite est 0,24 ;
la probabilité que le lance-balle envoie une balle coupée à gauche est 0,235.
Si le lance-balle envoie une balle coupée, quelle est la probabilité qu'elle soit envoyée à droite ?
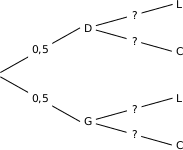
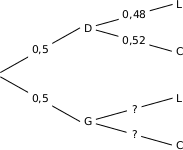
Soient les événements :
D : « La balle est lancée à droite » ;
G : « La balle est lancée à gauche » ;
L : « La balle est liftée » ;
C : « La balle est coupée ».
On peut faire un arbre pour modéliser la situation :
Il s'agit de calculer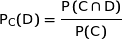 
.
Pour effectuer ce calcul nous avons besoin de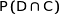 
. Pour l'obtenir nous complétons « les branches du haut » de l'arbre.
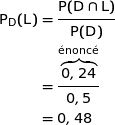
Donc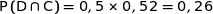 
.
Pour calculer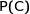 
on utilise la formule des probabilités totales.
Les événements D et G forment une partition de l'univers et on a :
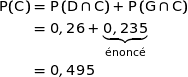
Finalement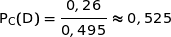 
.
