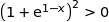Sujet et corrigé de l'exercice 3 du bac S de maths de mai 2016 au Liban
Cacher les corrigés
On considère la fonction 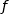 définie sur l'intervalle
définie sur l'intervalle 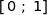 par :
par :
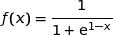
Partie A
1. Etudier le sens de variation de la fonction 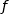 sur l'intervalle
sur l'intervalle 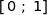 .
.
La fonction 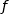 est dérivable sur
est dérivable sur 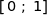 et pour tout
et pour tout 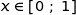 on a :
on a :
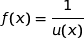
où 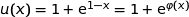
Donc 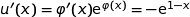
Enfin 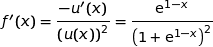
Pour tout 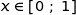 :
:
donc 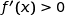 .
.
Il en résulte que 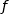 est croissante sur l'intervalle considéré.
est croissante sur l'intervalle considéré.
2. Démontrer que pour tout réel 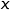 de l'intervalle
de l'intervalle 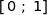 ,
, 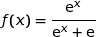 (on rappelle que
(on rappelle que 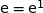 ).
).
Pour tout 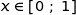 :
:
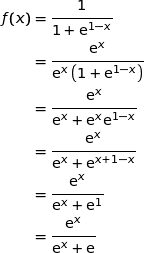
3. Montrer alors que 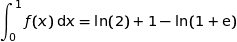 .
.
Pour calculer l'intégrale proposée nous avons besoin d'une primitive de 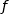 .
.
Pour en trouver une nous utilisons l'expression :
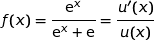
avec 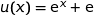 .
.
On remarque de plus que pour tout 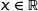 ,
, 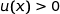 .
.
Donc une primitive sur 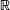 de
de 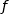 est définie par
est définie par 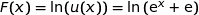 .
.
Par suite :
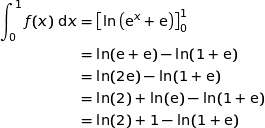
Partie B
Soit  un entier naturel. On considère les fonctions
un entier naturel. On considère les fonctions 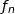 définies sur
définies sur 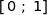 par:
par:
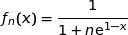
On note 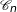 la courbe représentative de la fonction
la courbe représentative de la fonction 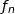 dans le plan muni d'un repère orthonormé.
dans le plan muni d'un repère orthonormé.
On considère la suite de terme général
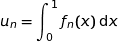
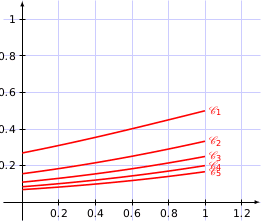
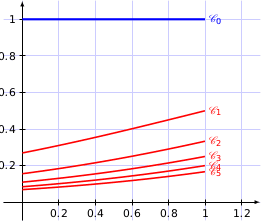
1. On a tracé les courbes représentatives des fonctions 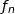 pour
pour  variant de 1
à 5. Compléter le graphique en traçant la courbe
variant de 1
à 5. Compléter le graphique en traçant la courbe  représentative de la fonction
représentative de la fonction 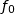 .
.
Pour tout 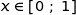 ;
; 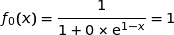 .
.
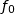 est la fonction constante 1 sur
est la fonction constante 1 sur 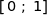 . Sa courbe représentative
. Sa courbe représentative 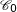 est le segment de droite dessiné sur le graphique ci-dessous :
est le segment de droite dessiné sur le graphique ci-dessous :
2. Soit  un entier naturel, interpréter graphiquement
un entier naturel, interpréter graphiquement 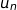 et préciser la valeur de
et préciser la valeur de 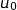 .
.
Pour tout entier naturel  et pour tout
et pour tout 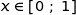 ,
, 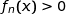 . Du coup
. Du coup 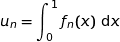 représente l'aire du domaine (en u.a.) délimité par :
représente l'aire du domaine (en u.a.) délimité par :
l'axe des abscisses ;
les droites d'équation
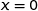 et
et 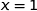 ;
;
la courbe
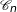 .
.
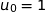 .
.
3. Quelle conjecture peut-on émettre quant au sens de variation de la suite 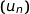 ?
?
Démontrer cette conjecture.
On conjecture que 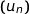 est décroissante car on observe que les aires des domaines successifs sont de plus en plus petites.
est décroissante car on observe que les aires des domaines successifs sont de plus en plus petites.
Pour tout entier naturel  :
:
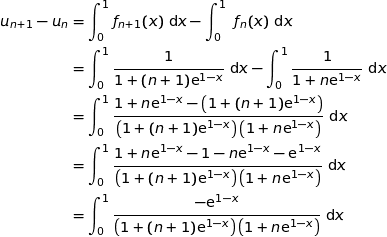
Or pour tout 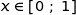 :
:
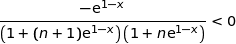 et par conséquent
et par conséquent 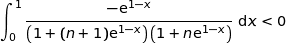 .
.
Donc pour tout entier naturel  ,
, 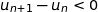 , ce qui prouve que
, ce qui prouve que 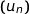 est décroissante.
est décroissante.
4. La suite 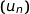 admet-elle une limite ?
admet-elle une limite ?
Pour tout entier naturel  et pour tout
et pour tout 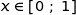 , on a
, on a 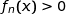 , donc
, donc 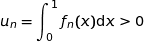 .
.
Finalement 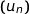 est une suite décroissante et minorée par 0, donc elle est convergente.
est une suite décroissante et minorée par 0, donc elle est convergente.