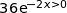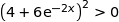Sujet et corrigé de l'exercice 4 du bac S de maths de mai 2016 au Liban
Cacher les corrigés
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant la réponse. Un point est attribué par réponse exacte justifiée. Une réponse non justifiée ne sera pas prise en compte et l'absence de réponse n'est pas pénalisée.
Sur le schéma ci-dessous on a représenté la courbe de densité d'une variable aléatoire
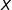qui suit une loi normale d'espérance 
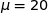. La probabilité que la variable aléatoire 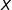soit
comprise entre 
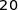et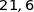 
est égale à 
.
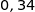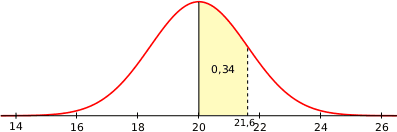
Affirmation 1 : La probabilité que la variable aléatoire
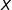appartienne à l'intervalle 
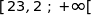vaut environ 0,046.Par symétrie :
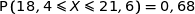.On reconnaît la probabilité de l'intervalle centré sur la moyenne à un sigma, donc
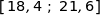c'est 
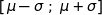et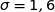 
.Par suite
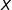suit la loi normale de moyenne 
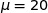et d'écart-type 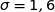.Avec la calculette on trouve :
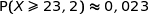.L'affirmation est FAUSSE.
Soit
un nombre complexe différent de 2. On pose :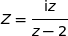
Affirmation 2 : L'ensemble des points du plan complexe d'affixe
tels que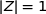 
est une
droite passant par le point A(1 ; 0).Pour tout
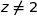on a :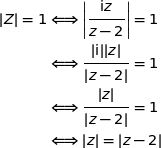
Soit M d'affixe
et B d'affixe 2. La dernière relation obtenue équivaut à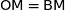 
(où 
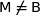car 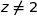).Du coup l'ensemble des points M cherchés est l'ensemble des points M équidistants de O et B : c'est la médiatrice de [OB]. Cette droite passe par le milieu de [OB] qui est A.
L'affirmation est VRAIE.
Affirmation 3 :
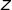est un imaginaire pur si et seulement si est réel.Pour tout complexe
:
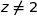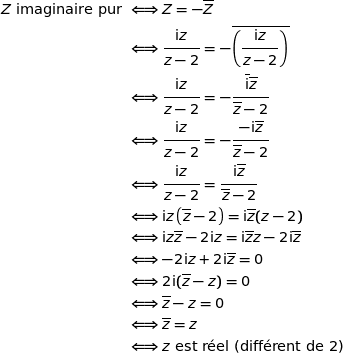
L'affirmation est VRAIE.
Soit
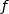la fonction définie sur 
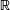par :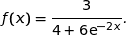
Affirmation 4 : L'équation
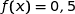admet une unique solution sur .
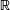Donc
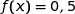admet une unique solution sur 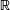.L'affirmation est VRAIE.
Affirmation 5 : L' algorithme suivant affiche en sortie la valeur
.
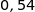Pour mieux comprendre la situation étudions les variations de
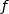.La fonction
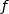est dérivable sur 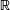et on a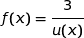 
où
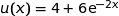et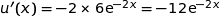 
.
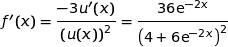.Pour tout
:donc
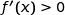et on a le tableau :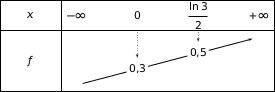
L'algorithme calcule les images successives par
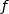en partant de 
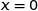et par pas de 0,01 avec arrêt dès que 
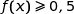.Comme la fonction est croissante il suffit d'observer ce qu'il se passe « juste avant »
.
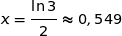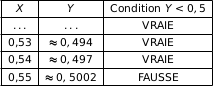
Donc en sortie l'algorithme affiche 0,55.
L'affirmation est FAUSSE.
