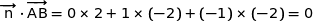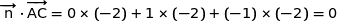Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2016 en métropole
Cacher les corrigés
Dans l'espace rapporté à un repère orthonormé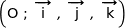 
on donne les points :
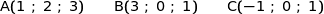
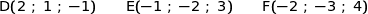
Pour chaque affirmation, dire si elle est vraie ou fausse en justifiant votre réponse. Une réponse non justifiée ne sera pas prise en compte.
Affirmation 1 : Les trois points A, B, et C sont alignés.
On considère les vecteurs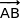 
et 
:
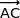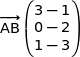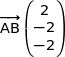
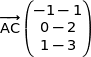soit 
soit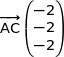 
On remarque que ces vecteurs ne sont pas colinéaires donc les points A, B et C ne sont pas alignés.
L'affirmation est FAUSSE.
Affirmation 2 : Le vecteur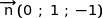 
est un vecteur normal au plan (ABC).
On calcule :
Ainsi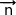 
est orthogonal aux deux vecteurs 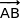et 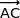non colinéaires du plan (ABC).
Cela montre que 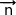est normal au plan (ABC).
L'affirmation est VRAIE.
Affirmation 3 : La droite (EF) et le plan (ABC) sont sécants et leur point d'intersection est le milieu du segment [BC].
On commence par déterminer un vecteur directeur de la droite (EF) :
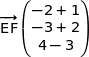soit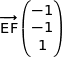 
Une représentation paramétrique de la droite (EF) est :
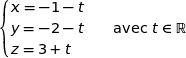
Une équation cartésienne du plan (ABC) s'écrit sous la forme :
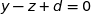
Comme le point A appartient au plan :
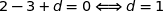
Donc (ABC) :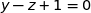 
Pour déterminer les coordonnées éventuelles du point d'intersection de la droite et du plan on résout maintenant le système :
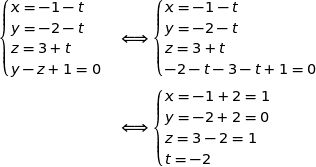
Donc la droite et le plan sont sécants et les coordonnées du point d'intersection sont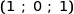 
.
Il reste à comparer ces coordonnées à celles du milieu de [BC] :
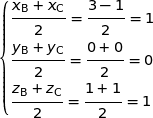
Comme cela coïncide, l'affirmation est VRAIE.
Affirmation 4 : Les droites (AB) et (CD) sont sécantes.
Un vecteur directeur de (AB) est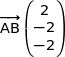
Un représentation paramétrique de (AB) est :
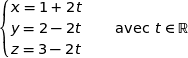
Un vecteur directeur de (CD) est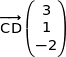 
.
Une représentation paramétrique de (CD) est :
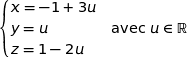
Pour savoir si les droites (AB) et (CD) sont sécantes on cherche leur point d'intersection éventuel en résolvant le système :
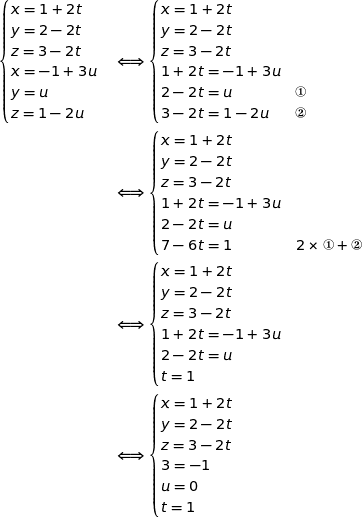
Donc le système n'a pas de solution et cela montre que (AB) et (CD) ne sont pas sécantes.
L'affirmation est FAUSSE.
