Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2016 en métropole
Cacher les corrigés
Lors d'un match de rugby, un joueur doit transformer un essai qui a été marqué au point E (voir figure ci-dessous) situé à l'extérieur du segment [AB].
La transformation consiste à taper le ballon par un coup de pied depuis un point T que le joueur a le droit de choisir n'importe où sur le segment [EM] perpendiculaire à la droite (AB) sauf en E. La transformation est réussie si le ballon passe entre les poteaux repérés par les points A et B sur la figure ci-dessous.
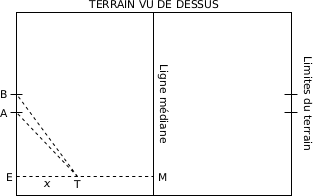
Pour maximiser ses chances de réussite, le joueur tente de déterminer la position du point T qui rend l'angle 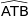 le plus grand possible.
le plus grand possible.
Le but de cet exercice est donc de rechercher s'il existe une position du point T sur le segment [EM] pour laquelle l'angle  est maximum et, si c'est le cas, de déterminer une valeur approchée de cet angle.
est maximum et, si c'est le cas, de déterminer une valeur approchée de cet angle.
Dans toute la suite, on note  la longueur ET, qu'on cherche à déterminer.
la longueur ET, qu'on cherche à déterminer.
Les dimensions du terrain sont les suivantes :
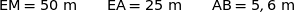
On note 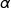 la mesure en radian de l'angle
la mesure en radian de l'angle 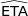 ,
, 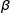 la mesure en radian de l'angle
la mesure en radian de l'angle  et
et 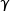 la mesure en radian de l'angle
la mesure en radian de l'angle 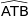 .
.
1. En utilisant les triangles rectangles ETA et ETB ainsi que les longueurs fournies, exprimer 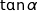 et
et 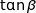 en fonction de
en fonction de 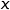 .
.
La fonction tangente est définie sur l'intervalle 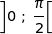 par
par 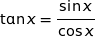 .
.
Dans le triangle ETA rectangle en E, en utilisant les relations trigonométriques élémentaires nous avons :
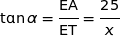
De même en travaillant dans ETB nous avons :
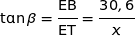
2. Montrer que la fonction tan est strictement croissante sur l'intervalle 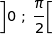 .
.
La fonction 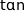 est dérivable sur
est dérivable sur 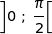 et nous avons :
et nous avons :
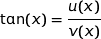 avec :
avec :
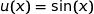 et
et 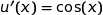
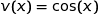 et
et 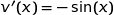
Donc :
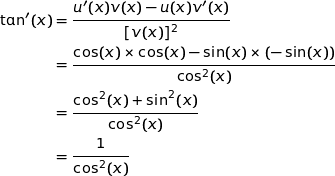
Il s'ensuit que pour tout  ;
; 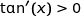 et donc que la fonction
et donc que la fonction 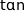 est strictement croissante sur l'intervalle considéré.
est strictement croissante sur l'intervalle considéré.
3. L'angle 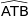 admet une mesure
admet une mesure 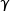 appartenant à l'intervalle
appartenant à l'intervalle 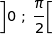 , résultat admis ici, que l'on peut observer sur la figure.
, résultat admis ici, que l'on peut observer sur la figure.
On admet que, pour tous réels 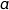 et
et 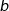 de l'intervalle
de l'intervalle 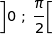 :
:
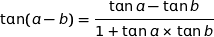
Montrer que 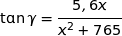 .
.
Vu la disposition des points sur la figure nous avons la relation : 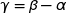 . Il s'ensuit que :
. Il s'ensuit que :
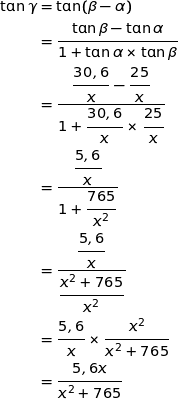
4. L'angle 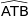 est maximum lorsque sa mesure
est maximum lorsque sa mesure 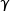 est maximale. Montrer que cela correspond à un minimum sur l'intervalle
est maximale. Montrer que cela correspond à un minimum sur l'intervalle 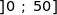 de la fonction
de la fonction 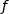 définie par :
définie par : 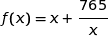 .
.
Montrer qu'il existe une unique valeur de 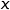 pour laquelle l'angle
pour laquelle l'angle 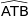 est maximum et déterminer cette valeur de
est maximum et déterminer cette valeur de  au mètre près ainsi qu'une mesure de l'angle
au mètre près ainsi qu'une mesure de l'angle  à
à 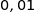 radian près.
radian près.
La fonction tangente étant croissante sur l'intervalle d'étude, 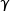 est maximum lorsque
est maximum lorsque 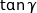 est maximum soit lorsque
est maximum soit lorsque 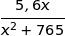 est maximum sur
est maximum sur 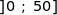 .
.
Par inverse 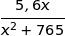 est maximum lorsque
est maximum lorsque 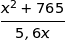 est minimum et on peut écrire :
est minimum et on peut écrire :

On remarque alors que les fonctions 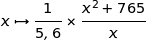 et
et 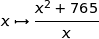 ont leur minimum atteints pour la même valeur de
ont leur minimum atteints pour la même valeur de 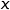 , donc finalement la mesure de
, donc finalement la mesure de 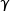 est maximale pour un minimum sur
est maximale pour un minimum sur  de la fonction définie par
de la fonction définie par 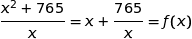 .
.
On étudie maintenant sur 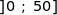 la fonction
la fonction 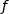 . Cette fonction est dérivable sur l'intervalle considéré et nous avons :
. Cette fonction est dérivable sur l'intervalle considéré et nous avons :
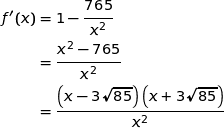
avec 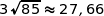 .
.
Compte tenu du signe du produit 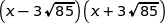 nous obtenons le tableau de variations :
nous obtenons le tableau de variations :
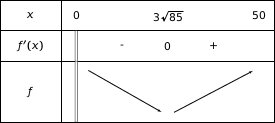
Cela met en évidence un uniquement minimum pour  sur
sur 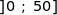 atteint pour
atteint pour 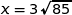 .
.
Donc 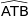 est maximum pour
est maximum pour 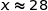 m et avec cette valeur :
m et avec cette valeur :
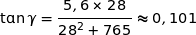
Avec la calculette on trouve 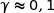 radians.
radians.
