Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2015 en Polynésie
Cacher les corrigés
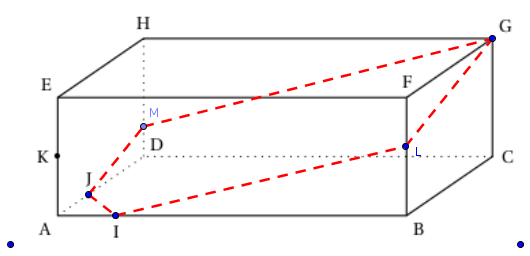
On considère le pavée droit ABCDEFGH ci-dessous, pour lequel :
, et
I, J et K sont les points tels que :
, et

On se place dans le repère orthonormé .
1. Vérifier que le vecteur de coordonnées est normal au plan (IJG).
On considère deux vecteurs non colinéaires du plan (IJG) :
soit
Les coordonnées de G sont et :
soit
Nous avons maintenant :
Du coup est orthogonal à et qui sont deux vecteurs non colinéaires du plan (IJG), donc est normal à ce plan.
2. Déterminer une équation du plan (IJG).
En exploitant le vecteur normal de la question précédente, une équation cartésienne du plan est de la forme :
Comme I appartient au plan on a :
Donc une équation cartésienne du plan considéré est :
.
3. Déterminer les coordonnées du point d'intersection L du plan (IJG) et de la droite (BF).
On commence par déterminer une représentation paramétrique de la droite (BF) où :
et
soit
Donc une représentation paramétrique est :
avec
On résout maintenant le système :
D'où
4. Tracer la section du pavé ABCDEFGH par le plan (IJG).
On ne demande pas de justification.
On place le point L sur le segment [BF] aux en partant de B.
On trace alors la ligne brisée JILG.
On trace la parallèle à (LG) qui passe par J, elle coupe [DH] en M.
On termine la section en traçant la ligne brisée : JMG.