Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2015 en Polynésie
Cacher les corrigés
Le plan complexe est rapporté à un repère orthonormé .
A tout point d'affixe du plan, on associe le point d'affixe définie par :
1. Un point est dit invariant lorsqu'il est confondu avec le point associé.
Démontrer qu'il existe deux points invariants.
Donner l'affixe de chacun de ces points sous forme algébrique, puis sous forme exponentielle.
Il s'agit de résoudre dans l'équation :
Le discriminant du trinôme est :
Donc l'équation admet deux solutions complexes conjuguées qui sont :
et
Forme exponentielle de
En factorisant par , il vient :
On cherche maintenant tel que :
On peut prendre , donc
Forme exponentielle de
Comme , on a directement :
2. Soit A le point d'affixe et B le point d'affixe
Montrer que OAB est un triangle équilatéral.
On remarque que A est d'affixe et B d'affixe .
Du coup , ce qui montre que OAB est un triangle équilatéral.
3. Déterminer l'ensemble des points d'affixe où et sont réels, tels que le point associé soit sur l'axe des réels.
Exprimons en fonction de et :
est réel équivaut à soit :
L'ensemble est constitué des points de la droite d'équation , c'est à dire l'axe des abscisses ainsi que des points de la droite d'équation .
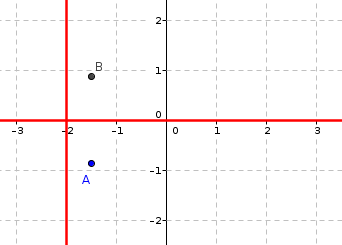
4. Dans le plan complexe, représenter les points A et B ainsi que l'ensemble .