Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2015 en Polynésie
Cacher les corrigés
Le directeur d'un zoo souhaite faire construire un toboggan pour les pandas. Il réalise le schéma suivant de ce toboggan en perspective cavalière.
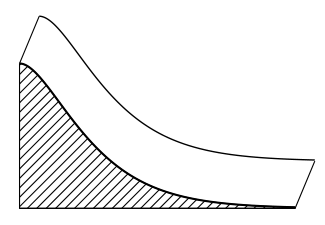
Partie A : Modélisation
Le profil de ce toboggan est modélisé par la courbe représentant la fonction définie sur l'intervalle par :
où et sont deux entiers naturels.
La courbe est tracée ci-dessous dans un repère orthonormé dont l'unité est le mètre.
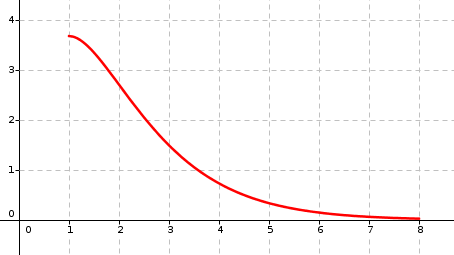
1. On souhaite que la tangente à la courbe en son point d'abscisse 1 soit horizontale.
Déterminer la valeur de l'entier .
La fonction est dérivable sur et pour tout :
avec :
;
;
Nous traduisons la contrainte donnée par soit :
Donc
2. On souhaite que le haut du toboggan soit situé entre 3,5 et 4 mètres de haut.
Déterminer la valeur de l'entier .
Cette fois la contrainte s'exprime par :
avec et .
L'unique entier tel que est .
Donc finalement :
Partie B : Un aménagement pour les visiteurs
On admet dans la suite que la fonction introduite dans la partie A est définie pour tout réel par :
Le mur de soutènement du toboggan sera peint par un artiste sur une seule face, hachurée sur le schéma en début d'exercice. Sur le devis qu'il propose, celui-ci demande un forfait de 300 euros augmenté de 50 euros par mètre carré peint.
1. Soit la fonction définie sur par :
Déterminer la fonction dérivéé de la fonction .
La fonction est dérivable sur et on a :
, avec :
;
;
2. Quel est le montant du devis de l'artiste ?
A la question précédente nous avons remarqué que , donc est une primitive de .
En outre, pour tout , .
Donc l'aire du domaine délimité par la courbe , l'axe des abscisses et les droites d'équations et s'exprime par :
Le montant du devis de l'artiste sera par conséquent de :
€.
Partie C : Une contrainte à vérifier
Des raisons de sécurité imposent de limiter la pente maximale du toboggan.
On considère un point de la courbe , d'abscisse différente de 1.
On appelle l'angle aigu formé par la tangente en à et l'axe des abscisses.
La figure suivante illustre la situation.
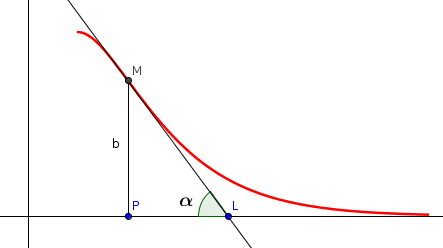
Les contraintes imposent que l'angle soit inférieur à 55 degrés.
1. On note la fonction dérivée de la fonction sur l'intervalle .
On admet que pour tout de l'intervalle , .
Etudier les variations de la fonction sur l'intervalle .
La fonction est dérivable sur et on a :
avec :
;
;
Pour tout , , donc le signe de est le même que celui de .
Ce binôme du premier degré s'annule pour ce qui nous donne le tableau de variations :
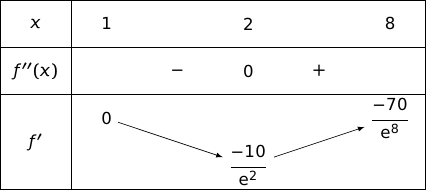
2. Soit un réel de l'intervalle et soit le point d'abscisse de la courbe .
Justifier que
Avec les notations du dessin fourni ; en utilisant les relations trigonométriques dans le triangle rectangle PML nous avons :
or est le coefficient directeur de la tangente en M à la courbe représentative de , donc .
Ainsi on a bien : .
3. Le toboggan est-il conforme aux contraintes imposées ?
On détermine le maximum sur de en exploitant l'étude de la fonction faite à la question 1.
On remarque que pour tout , ; donc le maximum de est obtenu lorsque est minimum soit pour et ce maximum pour vaut : .
En outre .
Donc nous avons : .
Or pour en degré appartenant à ; la fonction tangente est croissante ce qui entraîne que et donc que le toboggan est conforme.
