Sujet et corrigé de l'exercice 2 du bac S de maths d'avril 2016 à Pondichéry
Cacher les corrigés
L'objectif de cet exercice est de trouver une méthode pour construire à la règle et au compas un pentagone régulier.
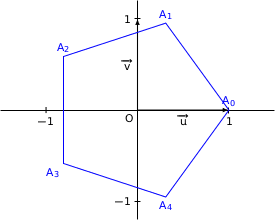
Dans le plan complexe muni d'un repère orthonormé direct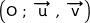 
, on considère le pentagone régulier 
de centre O tel que 
.
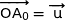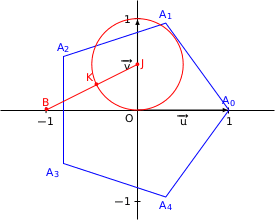
On rappelle que dans le pentagone régulier 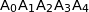ci-dessous :
les cinq côtés sont de même longueur ;
les points
, 
, 
, 
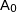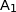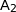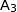et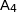 
appartiennent au cercle trigonométrique ;
pour tout entier
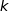appartenant à 
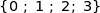on a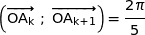 
.
1. On considère les points B d'affixe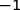 
et J d'affixe 
.
Le cercle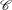 
de centre J et de rayon 
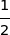coupe le segment [BJ] en un point K.
Calculer BJ, puis en déduire BK.
On désigne par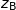 
l'affixe de B et par 
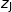l'affixe de J et on a :
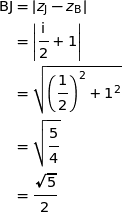
Le point K appartient au cercle de centre J et de rayon 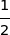, donc 
.
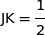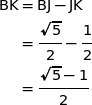
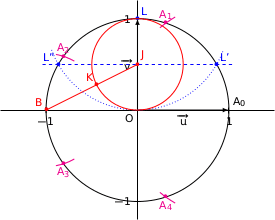
Un petit dessin pour mieux saisir la situation :
2.
a) Donner sous forme exponentielle l'affixe du point .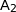
Justifier brièvement.
Pour le module c'est 1, puisque le point 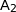est sur le cercle trigonométrique.
Pour un argument on remarque que :
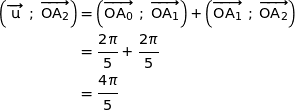
Ainsi l'affixe du point 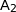peut s'écrire :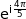 
b) Démontrer que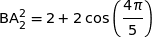 
.
L'affixe de 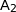est 
.
c) Un logiciel de calcul formel affiche les résultats ci-dessous, que l'on pourra utiliser sans justification :
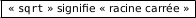
En déduire, grâce à ces résultats, que 
.
En utilisant la ligne 1 du logiciel de calcul formel on a :
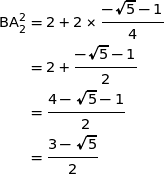
Maintenant en utilisant la ligne 2 du logiciel de calcul formel on obtient :
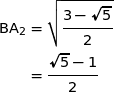
Le résultat obtenu coïncide avec le résultat obtenu pour BK, donc on a bien .
3. Dans le repère construire à la règle et au compas un pentagone régulier. N'utiliser ni le rapporteur ni les graduations de la règle et laisser apparents les traits de construction.
On commence par construire le cercle trigonométrique et on place le point
.
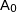On place le point L de coordonnées
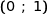; le cercle de centre L et de rayon 1 coupe le cercle trigonométrique en L' et L'' ; la droite (L'L'') coupe [OL] en son milieu ce qui donne le point J.
On place le point B et on trace le cercle de centre J et de rayon
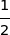, puis l'intersection avec [BJ] donne le point K.
On pique le compas en B et l'intersection du cercle de centre B et de rayon BK avec le cercle trigonométrique donne les points
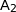et .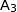
On pique maintenant le compas en
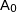et l'intersection du cercle de centre 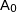et de rayon 
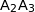avec le cercle trigonométrique donne les points 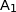et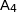
Il reste à joindre les points
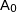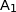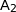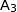, , , et 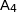pour obtenir le pentagone.
